Цей термін має також інші значення див. Рух.
Незважаючи на те, що рух визначається на всіх метричних просторах, цей термін більше поширений в геометрії Евкліда і суміжних областях. У метричній геометрії (зокрема, в ріманової геометрії) частіше говорять: изометрия простору в себе. У загальному випадку метричного простору (наприклад, для неплоского ріманова різноманіття) руху можуть існувати далеко не завжди.
В Евклідовому (або псевдоевклідовом) просторі рух автоматично зберігає також кути, так що зберігаються всі скалярні твори.
Далі в цій статті розглядаються ізометрії тільки евклидова точкового простору.
Власні і невласні руху
Власні руху зберігають орієнтацію простору E. невласні - замінюють її на протилежну [2]. Іноді власні і невласні руху називають відповідно переміщеннями і антіперемещеніямі [3].
Будь-яке рух n мірного евклідового точкового простору E може бути однозначно визначено вказівкою ортонормированного репера (O '; e 1'. .... E n '). , \ Ldots, e '_),> в який при даному русі переходить заздалегідь обраний в просторі E ортонормованій репер (O; e 1. .... E n). , \ Ldots, e _).> При цьому в разі власного руху новий репер орієнтований так само, як і вихідний, а в разі невласного руху новий репер орієнтований протилежним чином. Рухи завжди зберігають відстані між точками простору E (т. E. Є ізометрію), причому ніяких інших ізометрій, крім власних і невласних рухів, не існує [4].
У механіці в поняття «рух» вкладається інший зміст; зокрема, воно завжди розглядається як безперервний процес, що відбувається протягом певного проміжку часу (див. механічний рух). Якщо, слідуючи П. С. Александрову. називати безперервним рухом такий рух простору E. яке безперервно залежить від параметра t ∈ [t 0. t 1], t _]> (при n = 3 в механіці це відповідає руху абсолютно твердого тіла), то ортонормованій репер (O '; e 1 '. .... en'), \ ldots, e '_)> може бути отриманий безперервним рухом з ортонормированного репера (O; e 1. .... en), \ ldots, e _)> тоді і тільки тоді, коли обидва репера орієнтовані однаково [5].
Приватні види ізометрій
Будь-який рух прямий є або паралельне перенесення (що зводиться до зсуву всіх точок прямої на один і той же вектор, що лежить на цій же прямій), або відображення відносно деякої точки, взятої на даній прямій. У першому випадку рух є власним, у другому - невласних [6].
На площині
Будь-який рух площині відноситься до одного з наступних типів [2]:
Рухи перших двох типів - власні, останніх двох - невласні [7].
У тривимірному просторі
Будь-який рух тривимірного простору відноситься до одного з наступних типів [2]:
- Паралельний перенос;
- поворот;
- Гвинтовий рух - суперпозиція повороту щодо деякої прямої і перенесення на вектор, паралельний цій прямій;
- Дзеркальна симетрія (відображення) щодо площини;
- Змінна симетрія - суперпозиція перенесення на вектор, паралельний площині, і симетрії щодо цієї площини;
- Дзеркальний поворот - суперпозиція повороту навколо деякої прямої і відображення відносно площини, перпендикулярної осі повороту.
Рухи перших трьох типів вичерпують клас власних рухів тривимірного простору (теоремі Шаля), а рухи останніх трьох типів є невласними [7].
В n-вимірному просторі
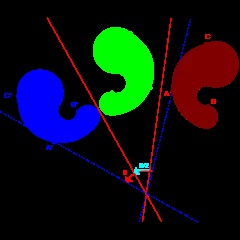
Суперпозиція двох відображень щодо непаралельних осей дає поворот