Тривимірна графіка, звана також ЗD-графікою, представляє в аксонометрической проекції об'ємне зображення поверхонь або фігур, які описуються або функціями двох змінних, або параметрично заданими координатами об'єктів. У цьому розділі містяться багато способів побудови тривимірних графіків, починаючи від простих контурних графіків і закінчуючи графіками поверхонь і фігур з функціональної забарвленням.
Побудова контурних графіків
Контурні графіки, або графіки ліній рівних висот, використовуються для відображення поверхонь на площині. Вони зручні для виявлення всіх екстремумів функцій в межах області графіка. Такі графіки є лініями перетину поверхні з січними горизонтальними площинами, розташованими паралельно один під одним. Вони часто використовуються в картографії.
Основними функціями і директивами для побудови контурних графіків є такі:
- ContourPlot [f ,,] - породжує контурний графік f як функції від х і у;
- ContourGraphics [array] - являє контурний графік масиву array;
- ListContourPlot [array] - формує контурний графік з масиву величин висот.
Цих функцій досить для побудови практично будь-яких монохромних графіків такого типу.
Для управління можливостями графічної функції ContourPlot використовуються опції, повний список яких виводить команда Options [ContourGraphics]. Крім уже розглянутих раніше опцій використовуються наступні:
- ColorFunction - задає забарвлення областей між лініями;
- Contours - задає число контурних ліній;
- ContourLines - задає промальовування явних (explicit) контурних ліній;
- ContourShading - задає затінення областей між контурними лініями;
- ContourSmoothing - задає згладжування контурних ліній;
- ContourStyle - задає стиль змальованих ліній для контурних графіків;
- MeshRange - задає області зміни х- і y-координат.
Малюнок 8.15 показує побудова контурного графіка з забарвленням проміжних областей між лініями. Забарвлення забезпечується опцією ColorFunction-> Hue. Опція ContourSmoothing -> True задає згладжування контурних ліній.
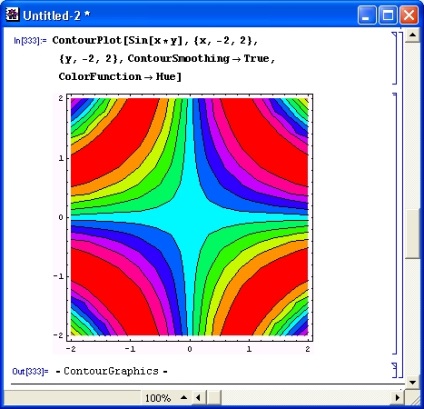
Мал. 8.15. Контурний графік поверхні sin (x у) з закраской областей між лініями рівного рівня відтінками сірого кольору
Наступний приклад (рис. 8.16) ілюструє ефективність застосування опції ContourShading. Якщо задати її значення рівним False, то заповнення простору між лініями буде відсутній. Таким чином, в даному випадку будуються тільки лінії рівного рівня.
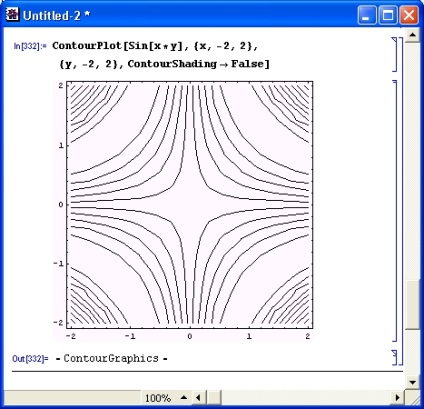
Мал. 8.16. Контурний графік, представлений тільки лініями рівного рівня
Іноді графік виявляється більш наочним, якщо прибрати побудова контурних ліній, але залишити зафарбовування областей між лініями. Такий варіант графіка більш кращий, якщо потрібно спостерігати якісну картину. Для побудови такого графіка треба використовувати опцію ContourLine-> False (рис. 8.17).
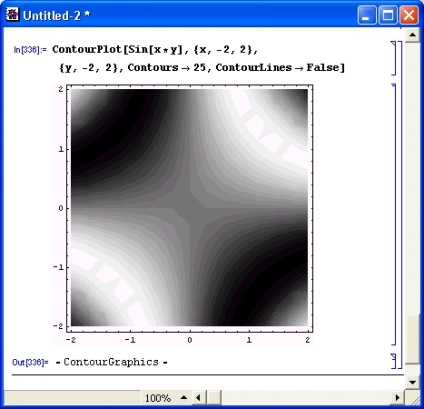
Мал. 8.17. Контурний графік без піній рівного рівня
Побудова графіків щільності
Функцією двох змінних f (x, у) може описуватися щільність деякої середовища. Для побудови графіків щільності використовуються наступні графічні функції:
- DensityGraphics [array] - є поданням графіка щільності;
- DensityPlot [f,,] - будує графік щільності f як функції від х і у;
- ListDensityPlot [array] - формує графік щільності з масиву величин висот.
З цими функціями використовується безліч (в основному вже розглянутих) опцій. Їх перелік можна отримати за допомогою функції Options.
Зовні графік щільності схожий на контурний графік. Однак для нього характерно виділення елементарних ділянок (з рівною щільністю) у формі квадратиків (рис. 8.18).
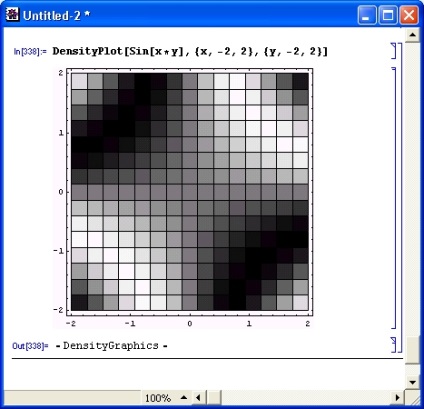
Мал. 8.18. Графік щільності
Побудова графіків поверхонь - функція Plot 3D
Функція двох змінних z = f (x, у) утворює в просторі деяку тривимірну поверхню або фігуру. Для їх побудови доводиться використовувати координатну систему з трьома осями координат: х, у і z. Оскільки екран дисплея плоский, то насправді об'ємність фігур лише імітується - використовується добре відомий спосіб наочного представлення тривимірних фігур за допомогою аксонометрической проекції.
Замість побудови всіх точок фігури зазвичай будується її каркасна модель, яка містить лінії розрізу фігури по взаємно перпендикулярним площинах. В результаті фігура представляється у вигляді сукупності безлічі криволінійних чотирикутників. Для додання фігурі більшої природності використовуються алгоритм видалення невидимих ліній каркаса і функціональна зафарбування чотирикутників з метою імітації бічного висвітлення постаті.
Для побудови графіків тривимірних поверхонь використовується основна графічна функція Plot 3D:
- Plot3D [f,] - будує тривимірний графік функції f змінних х і у;
- Plot3D [,,] - будує тривимірний графік, в якому висоту поверхні визначає параметр f, а затінення - параметр s.
На рис. 8.19 показаний приклад побудови поверхні, описуваної функцією двох змінних cos (x у) при х і у, що міняються від -3 до 3. Поверхня будується в вигляді каркаса з прямокутними осередками з використанням функціональної забарвлення. Всі опції задані за замовчуванням.
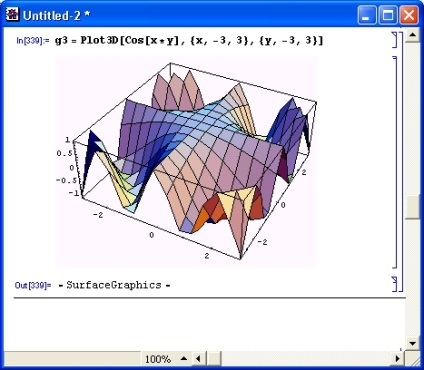
Мал. 8.19. Приклад побудови поверхні cos (xy) функцією Plot3D з опціями за замовчуванням
Цей графік вважатимемо вихідним для демонстрації його модифікацій, одержуваних шляхом зміни опцій.
Опції і директиви тривимірної графіки
Для модифікації тривимірних графіків можуть використовуватися численні опції і директиви, список яких подано в додатку. Їх застосування дозволяє будувати велику кількість графіків різних типів навіть при завданні однієї і тієї ж поверхні. Як приклад розглянемо окремі кадри документа, який демонструє вплив опцій на вигляд тривимірної математичної поверхні.
На рис. 8.20 показана вихідна поверхня (див. Рис. 8.19), побудована із застосуванням опції PlotPoint-> 50. Це означає, що поверхня по кожній осі ділиться на 50 частин (у вихідному графіку за замовчуванням використовується розподіл на 10 частин). Масштаб по вертикалі задається автоматично, з тим щоб всі висоти поверхні не обмежувалися.
На рис. 8.21 показана та ж поверхню, отримана із застосуванням опції PlotRange->, зрізаючого верхню частину поверхні (точки з координатами вище 0.5). Графік поверхні при цьому істотно змінюється (порівняйте з рис. 8.20).
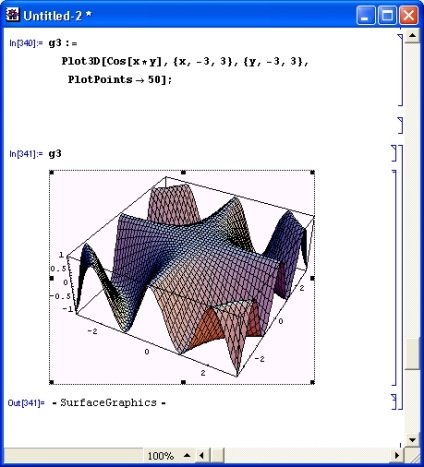
Мал. 8.20. Поверхня рис. 8.19 з великим числом осередків
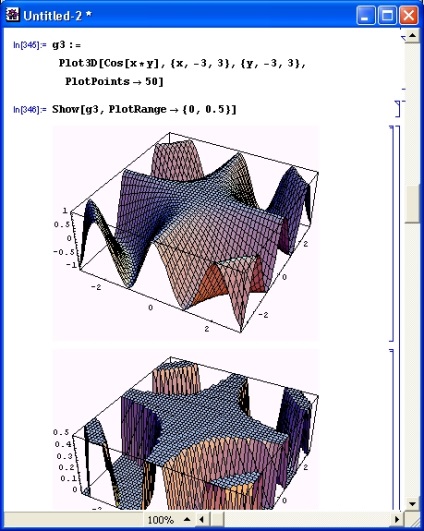
Мал. 8.21. Математична поверхню з відтятою верхньою частиною
Опція Boxed -> False видаляє обмежують рамки, що утворюють «ящик», в який вписується побудована тривимірна поверхня (рис. 8.22). Залишаються лише координатні осі.
Опція Viewpoint дозволяє включити при побудові відображення перспективи і змінювати кути, під якими розглядається фігура. Малюнок 8.23 ілюструє застосування цієї опції.
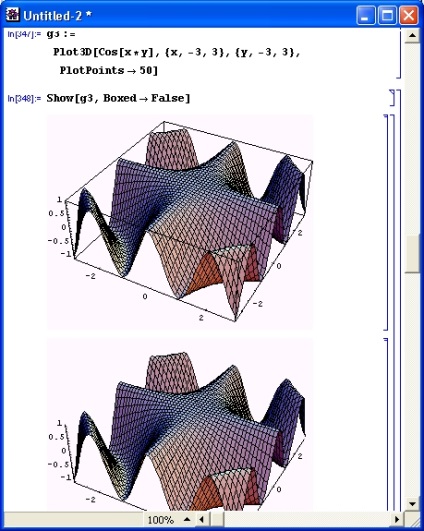
Мал. 8.22. Побудова тривимірної поверхні без обмежувального «ящика»
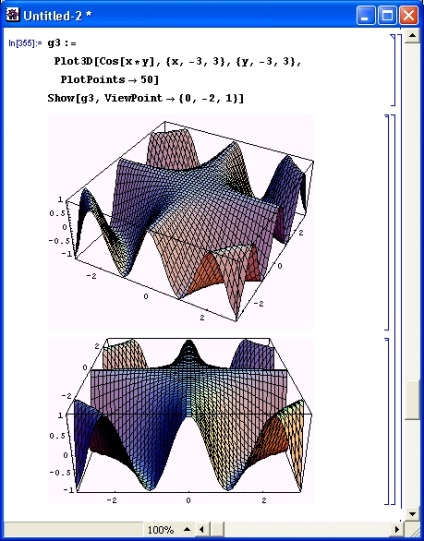
Мал. 8.23. Математична поверхню, побудована з урахуванням перспективи
Опція Mesh -> False дозволяє видалити лінії каркаса фігури. Нерідко це надає особі більш природний вигляд (рис. 8.24) - зазвичай ми спостерігаємо такі фігури без ліній каркаса.
У ряді випадків, навпаки, саме лінії каркаса несуть важливу інформацію. Система будує каркас тривимірних поверхонь двома способами - з використанням і без використання алгоритму видалення невидимих ліній. Малюнок 8.25 показує результат побудови при використанні алгоритму видалення невидимих ліній. Неважко помітити, що в цьому випадку поверхня виглядає досить естетично навіть без застосування функціональної зафарбовування.
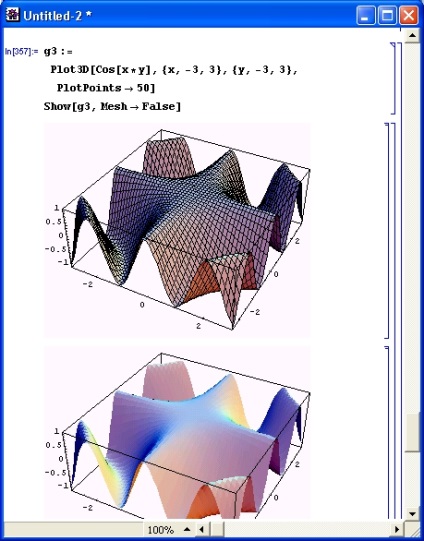
Мал. 8.24. Математична поверхню з віддаленими лініями каркаса
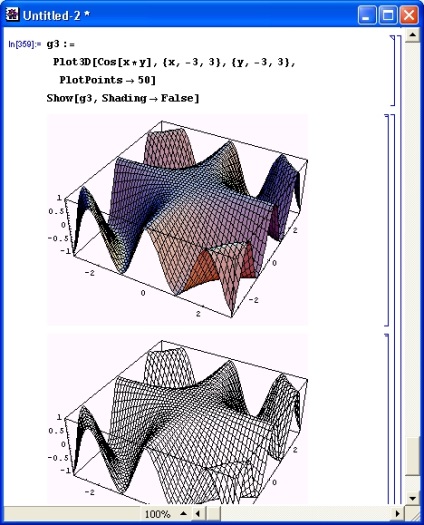
Мал. 8.25. Побудова каркаса математичної поверхні з використанням алгоритму видалення невидимих ліній
На рис. 8.26 показано побудову каркаса без видалення невидимих ліній. Такий вид математична поверхня має, якщо уявити її побудованої з тонких зволікань, що висять в просторі. Це дає додаткову інформацію про просторової фігурі, але естетично вона виглядає гірше, ніж фігура, побудована із застосуванням алгоритму видалення невидимих ліній каркаса.
Таким чином, як і раніше, застосування опцій дозволяє легко керувати характером і типом графіків, надаючи їм вигляд, зручний для заданого застосування. На рис. 8.27 показаний приклад побудови тривимірного графіка із застосуванням одночасно декількох опцій.
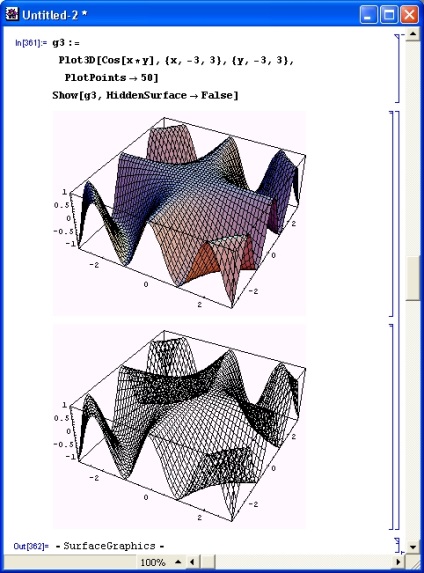
Риc. 8.26. Побудова каркаса математичної поверхні без використання алгоритму видалення невидимих ліній
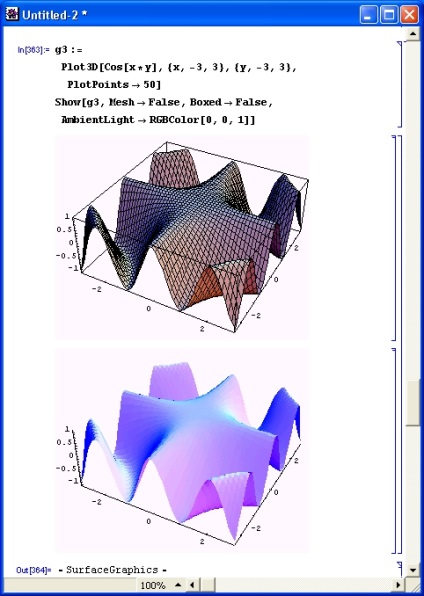
Риc. 8.27. Приклад побудови тривимірного графіка з декількома опціями
Наведені приклади найбільш наочно показують, наскільки легко модифікуються графіки за допомогою різних опцій. Зрозуміло, є безліч можливостей для інших модифікацій, які користувач може випробувати самостійно.
У розділі програми, присвяченому даному уроку, зазначений ряд додаткових директив і опцій тривимірної графіки. З їх допомогою можна розширити можливості побудови графіків. Читачеві рекомендується самостійно побудувати графіки ряду поверхонь з використанням різних опцій.
Графічна функція ListPlot3D
Часто тривимірна поверхня задається масивом своїх висот (аплікат). Для побудови графіка в цьому випадку використовується графічна функція ListPlotSD:
- ListPlot3D [array] - будує тривимірний графік поверхні, представленої масивом значень висот;
- ListPlot3D [array, shades] - будує графік так, що кожен елемент поверхні штрих (затінюється) згідно специфікації shades.
Plot Joined - додаткова опція для ListPlot, яка вказує, чи слід з'єднувати лінією точки, нанесені на графік.
Приклад застосування функції ListPlotSD показаний на рис. 8.28. Графік побудований за даними таблиці tS, формує значення аплікат поверхні, яка описується функцією cos (xy).
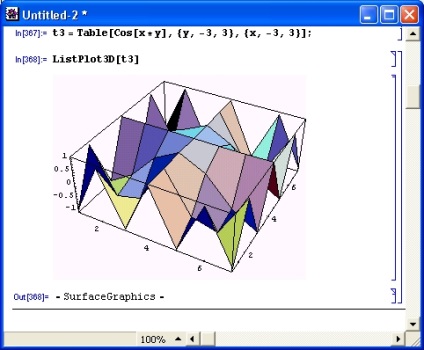
Мал. 8.28. Приклад застосування функції ListPlotSD
Застосовуючи описані в цьому розділі графічні функції разом з їх - опціями, директивами і примітивами, можна будувати величезну кількість типів тривимірних графіків. Однак багато такі графіки можуть створюватися за допомогою додаткових функцій, що входять в пакет розширення Graphics. Він описаний в уроці 13.
Командою Options [ListPlot3D] можна вивести повний список опцій даної функції, щоб використовувати їх для модифікації графіків, які будує ця функція.