лексикографічний критерій
Ситуація, в якій різниця між впорядкованими критеріями настільки велика, що наступний в цьому ряду критерій розглядається тільки в тому випадку, якщо порівнювані альтернативи невиразні по старшим критеріям. Такий вибір отримав назву лексикографічного впорядкування альтернатив, оскільки цей метод використовується при упорядкуванні слів в різних словниках. Найбільш часто МОЗ з таким жорстким упорядкуванням приватних критеріїв за важливістю виникає при послідовному введенні додаткових критеріїв в звичайні скалярні задачі оптимізації, які можуть мати неєдиний рішення. Нехай, наприклад, завдання з одним критерієм F1 має кілька рішень. Такий стан часто виникає в задачах лінійного програмування, дискретного програмування. При цьому для остаточного вибору можна використовувати другий, додатковий критерій F2 і відшукувати рішення, яке звертає в мінімум критерій F1 і доставляє критерію F2 найменше значення. Якщо і другий критерій не виділяє єдине рішення, то можна ввести третій критерій F3 і т.д.
Метод рівності приватних критеріїв
Критерії працюють на принципі компромісу, заснованого на ідеї рівномірності. Грунтуючись на ідеї рівномірного компромісу, намагаються знайти такі значення змінних X, при яких нормовані значення всіх приватних критеріїв стають рівними між собою, тобто
З урахуванням вагових коефіцієнтів важливості приватних критеріїв вираз (3) запишеться у вигляді
Зам. При великому числі приватних критеріїв через складність взаємозв'язків іноді важко домогтися виконання співвідношень (3) і (4).
Критерій Байеса-Лапласа
Цей критерій передбачає, що можливим станам природи можна приписати певну ймовірність їх настання і, визначивши математичне очікування виграшу для кожного рішення, вибрати те, яке забезпечує найбільше значення виграшу:
Критерій Байеса-Лапласа пред'являє до ситуації, в якій приймається рішення, наступні вимоги:
ймовірності появи станів В j відомі і не залежать від часу;
рішення реалізується (теоретично) нескінченно багато разів;
для малого числа реалізацій рішення допускається деякий ризик.
Метод головного критерію. лексикографічний критерій
Метод головного критерію
Існує один, часто вживаний спосіб звести многокритериальную завдання до однокритерійним - це виділити один (головний, основний) критерій F1 і прагнути його звернути в максимум (мінімум), а на решту F2. F3. Fm приватні критерії накласти тільки деякі обмеження, зажадавши, щоб вони були не менше (більше) якихось заданих величин.
Ситуація, в якій різниця між впорядкованими критеріями настільки велика, що наступний в цьому ряду критерій розглядається тільки в тому випадку, якщо порівнювані альтернативи невиразні по старшим критеріям. Такий вибір отримав назву лексикографічного впорядкування альтернатив, оскільки цей метод використовується при упорядкуванні слів в різних словниках. Найбільш часто МОЗ з таким жорстким упорядкуванням приватних критеріїв за важливістю виникає при послідовному введенні додаткових критеріїв в звичайні скалярні задачі оптимізації, які можуть мати неєдиний рішення. Нехай, наприклад, завдання з одним критерієм F1 має кілька рішень. Такий стан часто виникає в задачах лінійного програмування, дискретного програмування. При цьому для остаточного вибору можна використовувати другий, додатковий критерій F2 і відшукувати рішення, яке звертає в мінімум критерій F1 і доставляє критерію F2 найменше значення. Якщо і другий критерій не виділяє єдине рішення, то можна ввести третій критерій F3 і т.д.
Ухвалення рішення в умовах ризику з можливістю проведення експерименту
Дерево, на якому вказані всі етапи процесу прийняття рішень - дерево рішень. Гілки дерева відповідають можливим альтернативам, а вершини - виникаючих ситуацій. Позиції, в яких хід робить керівник групи, зображені прямокутником; позиції, в яких хід робить природа, - гуртком.
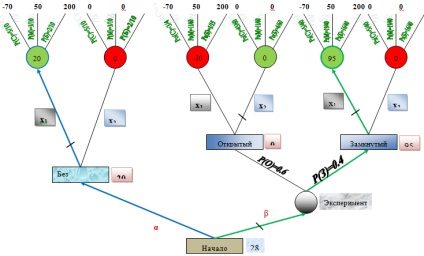
Гра протікає в такий спосіб. У початковій позиції хід робить керівник групи. Він повинен прийняти рішення - α або β. Якщо він відмовився від експерименту, то гра переходить в наступну позицію, в якій керівник групи повинен прийняти рішення: x1 або x2. Якщо ж він вирішує проводити експеримент, то гра переходить в позицію, в якій хід робить природа, вибираючи один зі станів Про або З, відповідних можливих результатів експерименту, і т. Д. Гра закінчується тоді, коли вона переходить в остаточну позицію (т. е. вершину дерева).
Крок 2. Для кожного рішення, яке є ходом природи треба знайти ймовірність цього ходу. Якщо це для позиції природи, шлях, що з'єднує її з з початковою позицією, не проходить через позицію (Е), яка б означала проведення експерименту, то ймовірності станів Р (С), Р (М) і Р (Б) є безумовними (додосвідні).
Якщо ж для позиції природи шлях, що з'єднує її з початковою позицією, проходить через позицію (Е), то ймовірності станів середовища стають умовними ймовірностями і знаходяться за формулами.
Крок 3. Зробимо оцінку всіх позицій дерева гри, "спускаючись" від кінцевих позицій до початкової. Оцінкою позиції служить очікуваний виграш в цій позиції.
У кожній позиції гравець позначає рискою ту гілку дерева, яка призводить до позиції, що має максимальну оцінку.
Про
Без проведення експерименту. Вибираємо максимальне значення з (20, 0). Воно дорівнює 20.
Брати до рис. 1. Отримуємо, що в початковій позиції очікуваний прибуток без проведення експерименту (альтернатива α) - 20 одиниць; очікуваний прибуток з проведенням експерименту (альтернатива β) - 28 одиниць. Таким чином, доцільним є рішення - проводити експеримент (сейсморозвідку). Далі, якщо експеримент покаже, що грунт відкритий, то буріння проводити не слід, а якщо замкнутий, то потрібно бурити.
2 - гілка: 0
3
З проведенням експерименту.
Вибираємо максимальне значення з
(-30, 0, 95, 0). Воно дорівнює 95.
- гілка :? ? = -30
6 - гілка: 0
Як випливає з умови задачі, значення в 95 одиниць ми можемо отримати з ймовірністю 0.4. Отже, очікуваний виграш буде дорівнює 0.4 * 95 = 38 одиницям. Віднімаємо витрати на проведення експерименту дорівнює 10 одиницям. В результаті отримаємо 28 одиниць.
Вагові коефіцієнти. Методи визначення вагових коефіцієнтів
Метод ранжирування. кожного експерта просять розставити приватні критерії проектованого об'єкта в порядку їх важливості. Цифрою 1 позначають найбільш важливий приватний критерій, цифрою 2 - наступний за важливістю приватний критерій і т.д.
, i = 1,2, ..., m.
- (I = 1,2. M) - формула для обчислення вагових коефіцієнтів i за методом ранжирування.
Метод приписування балів
Цей метод заснований на тому, що експерти оцінюють важливість приватного критерію за шкалою [0-10]. При цьому дозволяється оцінювати важливість дробовими величинами або приписувати одну і ту ж величину з обраної шкали кількома критеріями.
де - сума i - го рядка.
rik - називають вагою, підрахованими для k - критерію i - м експертом. Звідси, враховуючи, що
Проблеми вирішення завдань векторної оптимізації
Нормалізація критеріїв. Так як приватні критерії мають різний фізичний зміст, тобто вимірюються в різних одиницях; масштаби їх не співмірні, тому неможливо порівняння якості отриманих результатів за кожним критерієм. Операція приведення масштабів локальних критеріїв до єдиного, зазвичай безрозмірного, носить назву нормалізації критеріїв.
Вибір принципу оптимальності, тобто потрібно визначити правило, яке дозволило б сказати яке рішення краще. Принцип оптимальності - основна проблема векторної оптимізації.
Облік пріоритету критеріїв. Зазвичай з фізичного змісту задачі випливає, що локальні критерії мають різну важливість при вирішенні завдання, тобто один локальний критерій має якийсь пріоритет над іншим локальним критерієм. Це слід враховувати при виборі принципу оптимальності і визначенні області можливих рішень, віддаючи перевагу більш важливим критеріям.
Обчислення оптимуму ЗВО. Наразі досягнуто певні успіхи в області вирішення завдань математичного програмування (МП). Так за одними даними, методів однокритерійним оптимізації та їх модифікацій більше 500 (п'ятисот), за іншими - їх кількість перевалила за кілька тисяч! Але їх, як правило, не можна один до одного застосовувати до вирішення змо, тому що відомі приклади, коли обчислювальні алгоритми стають непридатними для вирішення завдань МП в результаті невеликих змін і доповнень до первісної задачі, тому постає проблема - обчислення оптимуму побудованої задачі векторної оптимізації. Однак зазначимо, що перераховані проблеми так чи інакше зводять многокритериальную завдання до однокритерійним, тобто зводять до проблеми обчислення оптимуму.
Розвиток методів вирішення ЗВО йде за трьома напрямками:
Заміна векторного критерію скалярним критерієм, тобто перехід до однокритерійним задачі оптимізації;
Послідовне вирішення кінцевого безлічі однокритеріальних завдань;
Звуження безлічі D з подальшим безпосереднім вибором оптимального рішення.