Нехай функція y = f (x) визначена на проміжку X. Візьмемо точку. Дамо значенням x прирощення. тоді функція одержить збільшення.
Визначення. Похідною функції y = f (x) називається границя відношення приросту функції до приросту незалежної змінної при прагненні останнього до нуля (якщо ця межа існує)
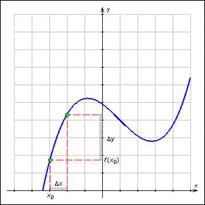
Знаходження похідної функції називається диференціюванням цієї функції.
Якщо функція в точці x має кінцеву похідну, то функція називається диференційованою в цій точці.
Функція, що диференціюється в усіх точках проміжку X, називається дифференцируемой на етомпромежутке.
Геометричний зміст похідної. похідна є кутовий коефіцієнт (тангенс кута нахилу) дотичній. проведеної до кривої y = f (x) в точці. тобто .
Тоді рівняння дотичної до кривої y = f (x) в точці має вигляд
Механічний зміст похідної. похідна шляху по часу є швидкість точки в момент:
Економічний зміст похідної: похідна обсягу виробленої продукції по часу є продуктивність праці в момент.
Залежність між безперервністю і
диференціюється
Теорема. Якщо функція y = f (x) диференційована в точці. то вона в цій точці неперервна.
Зворотній теорема невірна, тобто якщо функція неперервна в цій точці, то вона не обов'язково диференційована в цій точці.
Прикладом може служити функція y = | x |, безперервна в точці x = 0, однак вона має в ній «злам». Похідна цієї функції в точці x = 0 не існує, так як.
Таким чином, безперервність функції - необхідна, але недостатня умова дифференцируемости функції.
Схема обчислення похідної
Похідна функції може бути знайдена за такою схемою:
1. Дамо аргументу x прирощення і знайдемо розширене значення функції.
2. Знаходимо приріст функції.
3. Складаємо відношення.
4. Знаходимо межа цього відношення при. тобто (якщо ця межа існує).
Приклад 1. Знайти похідну функції.
1. Дамо аргументу x прирощення і знайдемо розширене значення функції.
2. Знаходимо приріст функції:
3. Складаємо відношення.
4. Знаходимо межа
1. Похідна постійної дорівнює нулю:.
2. Похідна аргументу дорівнює одиниці:.
3. Похідна суми дорівнює сумі похідних цих функцій
4. Похідна добутку двох диференційовних функцій дорівнює:
5. Постійний множник можна виносити за знак похідної
6. Похідна частки двох функцій, що диференціюються може бути знайдена за формулою:
7. Похідна складної функції дорівнює
Похідні основних елементарних функцій: