Криптографія з відкритим ключем
На відміну від симетричного ключа шифрування, ми не знаходимо історичне використання криптографії з відкритим ключем. Це відносно нова концепція.
Симетрична криптографія добре підходить для таких організацій, як уряду, військових і великих фінансових корпорацій були залучені в секретного зв'язку.
З поширенням більш неперевірених комп'ютерних мереж в останні кілька десятиліть, реальна необхідність відчувалася використовувати криптографію в ширшому масштабі. Симетричний ключ був знайдений, щоб бути не практично через проблеми, з якими вона стикається для управління ключами. Це призвело до відкритого ключа криптосистем.
Процес шифрування і дешифрування зображений на наступній ілюстрації -
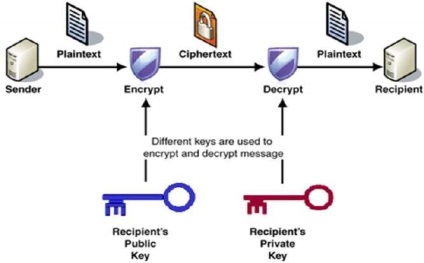
Найбільш важливі властивості ключової схеми громадського шифрування -
Різні ключі використовуються для шифрування і дешифрування. Це властивість, встановити цю схему відмінну від симетричною схеми шифрування.
Кожен приймач володіє унікальним ключ дешифрування, який зазвичай називають його закритим ключем.
Деякі гарантії справжності відкритого ключа необхідно в цій схемі, щоб уникнути підміни від противника в якості приймача. Як правило, цей тип криптосистеми включає довіреної третьої сторони, яка засвідчує, що конкретний відкритий ключ належить конкретній фізичній або юридичній особі тільки.
Алгоритм шифрування досить складна, щоб заборонити зломі шифру відкритий текст, з шифротекста і ключа шифрування (громадської).
Хоча приватні та публічні ключі пов'язані математично, не бути можливим обчислити закритий ключ з відкритого ключа. Насправді, інтелектуальна частина будь-якого відкритого ключа криптосистеми в проектуванні відносин між двома ключами.
Є три типи суспільних схем ключа шифрування. Ми обговоримо їх в наступних розділах -
RSA Cryptosystem
Це криптосистема є одним з вихідної системи. Він залишається найбільш зайнятих криптосистеми навіть сьогодні. Система була винайдена трьома учениміРівест, Аді Шамір і Льон Адлеман і. отже, це називається як RSA криптосистеми.
Ми бачимо два аспекти криптосистеми RSA, по-перше генерація пари ключів і по-друге алгоритмів шифрування і дешифрування.
Генерація RSA Key Pair
Кожна людина або партія, хто бажає взяти участь в зв'язку з використанням шифрування необхідно згенерувати пару ключів, а саме відкритий ключ і закритий ключ. Процес слідують в генерації ключів описана нижче -
Сформувати модуль RSA (п)
Виберіть два великих простих числа р і д.
Обчислити п = р * д. Для сильної непорушною шифрування, нехай п велика кількість, як правило, не менше 512 біт.
Знайти номер (Похідний е)
Число повинно бути більше 1 і менше. ніж (р - 1) (Q - 1).
Там не повинно бути загальним фактором для е і (р - 1) (д - 1), за винятком 1. Іншими словами, два числа е і (р - 1) (д - 1) взаємно прості.
Форма відкритого ключа
Пара чисел (п, е) утворюють відкритий ключ RSA і оприлюднений.
Цікаво, що хоча п є частиною відкритого ключа, труднощі в факторізующім велике просте число гарантує, що зловмисник не зможе знайти в кінцевий час двох простих чисел (р Q), що використовується для отримання п. Це сила RSA.
Генерація закритого ключа
Закритий ключ d обчислюється з р, д, е. Для цього п і е, є унікальне число d.
Число d є зворотним по модулю е (р - 1) (д - 1). Це означає, що d це число менше, ніж (р - 1) (Q - 1) таким чином, що при множенні на е, дорівнює 1 по модулю (р - 1) (д - 1).
Це співвідношення записується математично наступним чином -
Розширена алгоритм Евкліда приймає р, д, е і в якості вхідних даних і дає д виході.
Приклад генерації пари ключів RSA наведено нижче. (Для простоти розуміння, прості числа р і д взяті тут малі значення. Практично, ці значення дуже високі).
Нехай два штриха буде р = 7 і д = 13. Таким чином, модуль п = PQ = 7 х 13 = 91.
Вибір е = 5, який є коректним вибором, так як не існує числа, що є загальним фактором, 5 і (р - 1) (Q - 1) = 6 × 12 = 72, за 1, за винятком.
Пара чисел (п, е) = (91, 5) формує відкритий ключ і можуть бути зроблені доступними для тих, кого ми хочемо, щоб мати можливість відправити нам зашифровані повідомлення.
Вхідний р = 7, д = 13, і е = 5 для розширеного алгоритму Евкліда. Вихідний сигнал буде d = 29.
Переконайтеся, що d обчислюється правильно шляхом обчислення -
Отже, загальний ключ (91, 5) і закритих ключів (91, 29).
Шифрування і дешифрування
Після того, як пара ключів згенеровано, процес шифрування і дешифрування є відносно простими і в обчислювальному відношенні легко.
Цікаво відзначити, що RSA безпосередньо не працюють з рядками бітів, як і в випадку з ключем шифрування симетричним. Він працює по модулю п числа. Отже, необхідно, щоб представити відкритого тексту у вигляді серії чисел, менших п.
шифрування RSA
Припустимо, що відправник хотів би відправити деякі текстове повідомлення кому-то, чий відкритий ключ (п, е).
Потім відправник являє собою відкритий текст як послідовність чисел, менших, ніж п.
Для шифрування першого відкритого тексту P, який являє собою число по модулю п. Процес шифрування є простий математичний крок, як -
Іншими словами, шифротекст З дорівнює відкритого тексту P, помноженої на собі е раз, а потім відновлюють по модулю п. Це означає, що С також дещо менше, ніж п.
Повертаючись до нашого прикладу генерації ключів з відкритим текстом P = 10, ми отримуємо зашифрованого C -
RSA дешифрування
Процес розшифрування для RSA також дуже проста. Припустимо, що одержувач відкритого ключа пари (п, е) отримав зашифрованого C.
Приймач піднімає C до сили свого секретного ключа д. Результат по модулю п буде відкритим текстом П.
Повертаючись знову до нашого числовому прикладі, шифротекст C = 82 буде отримати розшифровані на номер 10, з використанням секретного ключа 29 -
аналіз RSA
Безпека RSA залежить від сильних сторін двох окремих функцій. Криптосистема RSA є найбільш популярним відкритим ключем криптосистема сила якого заснована на практичній труднощі факторингових дуже великі числа.
Шифрування Функція - це розглядається як односторонньої функції перетворення відкритого тексту в шифрований і може бути скасовано лише з відома секретного ключа д.
Генерація ключа - Складність визначення секретного ключа з відкритого ключа RSA еквівалентно факторизации по модулю п. Зловмисник, таким чином, не може використовувати знання про відкритого ключа RSA для визначення секретного ключа RSA, якщо він не може враховувати п. Це також є функцією один із способів , переходячи від р і д значень за модулем п легко, але зворотне неможливо.
Якщо будь-яка з цих двох функцій доведені не в одну сторону, а потім RSA буде порушена. Насправді, якщо метод факторинг ефективно розвивається, то RSA більше не буде безпечна.
Сила шифрування RSA різко знижується від атак, якщо число р і д не великі прості числа і / або обраний відкритий ключ е невелике число.
ElGamal Cryptosystem
Поряд з RSA, є й інші криптосистеми з відкритим ключем, запропоновані. Багато з них засновані на різних версіях завдання дискретного логарифмування.
ElGamal криптосистема, називається еліптичної кривої Варіант, на основі дискретного логарифмування завдання. Він витягує силу з припущення, що дискретні логарифми не можуть бути знайдені в практичній терміни для заданого числа, в той час як зворотна операція потужності може бути обчислена ефективно.
Давайте пройти просту версію ElGamal, яка працює з числа по модулю р. У разі еліптичних кривих варіантів, вона заснована на абсолютно різних системах числення.
Генерація ElGamal пари ключів
Кожен користувач ElGamal криптосистеми генерує пару ключів через наступним чином -
Вибір великого простого числа р. У загальному випадку просте число від 1024 до 2048 біт довжини вибирається.
Вибір елемента генератора р
Це число повинне бути між 1 і р - 1, але не може бути будь-яка кількість.
Це генератор мультипликативной групи цілих чисел по модулю р. Це означає. що для будь-якого цілого т взаємно прості з р, існує ціле число до таке. що г к = мод п.
Наприклад, 3 є генератором групи 5 (Z 5 =).
Вибір секретного ключа. Закритий ключ х будь-яке число більше 1 і менше. ніж P-1.
Обчислювальна частина відкритого ключа значення у обчислюється з параметрів р, г і секретного ключа х наступним чином. -
Отримання відкритого ключа. Відкритий ключ ElGamal складається з трьох параметрів (р, г, у).
Наприклад, припустимо. що р = 17. і що г = 6 (Це може бути підтверджено. що 6 є генератором групи Z 17). Секретний ключ х може бути будь-яке число більше 1 і менше 71, тому ми вибираємо х = 5. Величина у обчислюється таким чином -
Таким чином, закритий ключ 62 і відкритий ключ (17, 6, 7).
Шифрування і дешифрування
Генерація пари ключів ElGamal порівняно простіше, ніж еквівалентний процес для RSA. Але шифрування і дешифрування трохи складнішим, ніж RSA.
ElGamal Шифрування
Припустимо, що відправник бажає послати відкритим текстом до кого-то, чий ElGamal відкритий ключ (р, г, у), а потім -
Відправник є відкритий текст у вигляді ряду чисел по модулю р.
Для шифрування першого відкритого тексту P, який представлений як число по модулю р. Процес шифрування для отримання зашифрованого C виглядає наступним чином -
- Випадковим чином генерують число до;
- Обчисліть два значення C1 і C2, де -
-
Надіслати зашифрований текст C, що складається з двох окремих значень (C1, C2), які були надіслані разом.
Звертаючись до нашого ElGamal наприклад генерування ключа, наведеного вище, відкритим текстом P = 13 шифрується таким чином -
- Випадковим породжують ряд, скажімо, до = 10
- Обчисліть два значення C1 і C2, де -
-
Відправлення зашифрованого тексту C = (C1, C2) = (15, 9).
ElGamal дешифрування
Для розшифровки зашифрованого (C1, C2) з використанням секретного ключа х, такі два кроки будуть прийняті -
Обчислюють модульне інверсію (С1) х по модулю р, що (С1) -x, як правило. називають коефіцієнтом дешифрування.
Отримайте відкритий текст, використовуючи наступну формулу -
У нашому прикладі, для розшифровки зашифрованого тексту C = (C1, C2) = (15, 9) з використанням секретного ключа х = 5, коефіцієнт дешифрування
Витяг відкритого тексту P = (9 × 9) по модулю 17 = 13.
аналіз ElGamal
В системі ElGamal, кожен користувач має секретний ключ х. і складається ізтрех компонентів відкритого ключа - простому модулю р, генератора г і громадського Y = г х помодулю р. Сила ElGamal заснована на складності завдання дискретного логарифмування.
Розмір захищений ключ зазвичай> 1024 біт. Сьогодні навіть 2048 біт використовуються довгі ключ. На передній швидкості обробки, Elgamal досить повільно, він використовується в основному для ключових протоколів аутентифікації. Завдяки більш високій ефективності обробки, Еліптичні варіанти кривої ElGamal стають все більш популярними.
Криптографія на еліптичних кривих (ECC)
Криптографія на еліптичних кривих (ECC) являє собою термін, який використовується для опису набір криптографічних засобів і протоколів, безпеку яких заснована на спеціальних версіях завдання дискретного логарифмування. Він не використовує чисел по модулю р.
ECC заснована на набори чисел, які пов'язані з математичними об'єктами називаються еліптичними кривими. Існують правила складання і обчислення кратних цих чисел, так само, як є для чисел по модулю р.
ECC включає в себе варіанти багатьох криптографічних схем, які були спочатку розроблених для модульних чисел, таких як шифрування ElGamal і алгоритм цифрового підпису.
Вважається, що дискретний логарифмирование набагато складніше в застосуванні до точок на еліптичній кривій. Це спонукає перехід від числа по модулю р до точок на еліптичній кривій. Також еквівалентний рівень безпеки може бути отриманий з більш короткими ключами, якщо ми використовуємо еліптичні варіанти кривої на основі.
Більш короткі ключі призводять до двох переваг -
- Зручність управління ключами
- ефективне обчислення
Ці переваги роблять еліптичної кривої на основі варіантів схеми шифрування вельми привабливим для застосування, де туги обчислювальні ресурси.
RSA і ElGamal Схеми - Для порівняння
Давайте коротко порівняти схеми RSA і ElGamal з різних аспектів.