Косим вигином називається такий вид вигину, при якому площина навантаження (силова лінія) згинального моменту не збігається ні з однією з головних осей інерції поперечного перерізу стержня X, Y (рис. 7.1, а, б).
При косому вигині діючі зовнішні сили (моменти) представляють їх проекціями на головні осі поперечного перерізу (рис. 7.1, б), тим самим зводять задачу до випадку поперечного вигину в двох головних площинах. З рис. 7.1, а, б видно, що:
Згинальні моменти в розрахунковому перерізі:
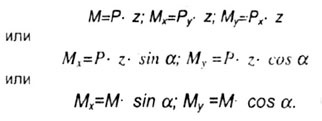
При обраному напрямку головних центральних осей інерції позитивним Октант буде перший октант (на рис. 7.1, а, б заштрихован).
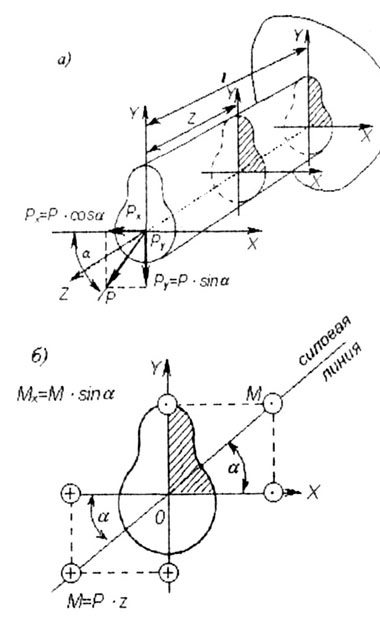
Правило знаків. Згинальні моменти в розрахунковому поперечному перерізі вважаються позитивними, якщо вони викликають у першому (заштрихованном) октанте напруги розтягнення.
Нормальні напруги в точках поперечного перерізу з поточними координатами х, у визначаються алгебраїчною сумою напруг, що викликаються изгибающими моментами М x і М y.
де J x і J y - моменти інерції поперечного перерізу відносно головних, центральних осей інерції перерізу X, Y, т. е. змінюються за лінійним законом. Рівняння нейтральної (нульової) лінії в перерізі знайдемо, прирівнявши
При х = 0 значення у = 0, т. Е. Пряма з кутовим коефіцієнтом k проходить через центр ваги поперечного перерізу.
При косому вигині нейтральна лінія являє собою пряму, що не перпендикулярна до площини згинального моменту. або, що одне і те ж, до силової лінії.
Силова лінія нахилена до осі X під кутом а, отже, її кутовий коефіцієнт дорівнює:
Кутовий коефіцієнт нейтральної лінії:
Так як в загальному випадку J x не дорівнює J y. то і k 1 не дорівнює - 1 / k, отже, нульова довжина не перпендикулярна силової лінії, а повернута в бік головної осі мінімального моменту інерції.
Нейтральна лінія розділяє поперечний переріз на дві зони:
- в якій діють тільки напруги розтягнення;
- в якій діють тільки напруги стиснення. Перший (заштрихований) квадрант (рис 7.1, а) знаходиться завжди в зоні дії напружень розтягу. Максимальні за величиною нормальні напруги знаходяться в точках поперечного перерізу максимально віддалених від нейтральної осі.
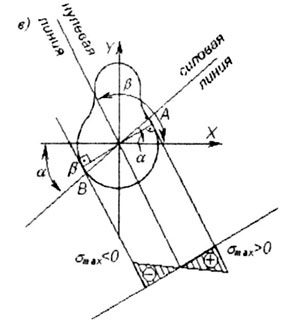
Максимальні за величиною напруги розтягнення виникають в точці А з координатами X a. Y л. а максимальні напруження стиску виникають в точці В з координатами X В. Y В (рис. 7.1, в):
Отримаємо епюру нормальних напружень в розрахунковому перерізі (7.1, в).
Умова міцності. Якщо матеріал стержня однаково працює на розтяг і на стиск, то умова міцності записується у вигляді:
Якщо матеріал стержня працює на розтяг і на стиск не однаково, то розрахунок проводиться окремо, т. Е. Перевіряються умови міцності:
Для поперечних перерізів, що мають дві осі симетрії:
де W x. W y - момент опору поперечного перерізу відносно головних, центральних осей інерції X, Y.
Прогини при косому вигині. Прогин кінця консолі від дії Р x спрямований по осі X і дорівнює:
Прогин від дії Р y спрямований по осі Y і дорівнює: