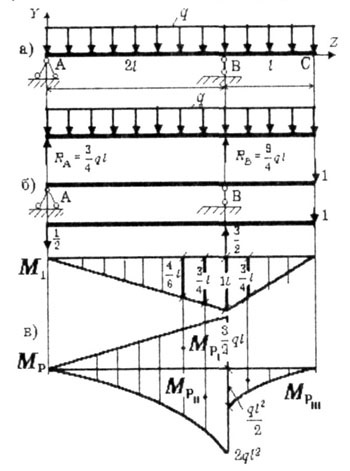
Визначимо прогин вільного кінця.
- Будуємо епюру згинальних моментів М p від заданої сили Р (рис. 6.4, а).
- Звільняємо балку від сили Р і потім у напрямку шуканого прогину на вільному кінці прикладаємо одиничну силу і будуємо від неї одиничну епюру згинальних моментів М 1 (рис. 6.4, б).
- Обчислюємо прогин вільного кінця за формулою (2). Для цього перемножуємо за способом Верещагіна епюри М p і М 1.
- Так як обидві епюри лінійні, байдуже на якій з них брати площу і на який ординату.
- Обидві епюри лежать по одну сторону осі, тому їх перемноження дає плюс.
Тепер визначимо прогин перерізу К. Епюра згинальних моментів від сили Р (рис. 6.5, а) залишиться та ж сама і буде лінійна на всьому протязі балки, а епюра від одиничної сили, прикладеної в перетині К (рис. 6.5, б) - ламана , тому, застосовуючи правило Верещагіна, беремо площа епюри М 1. а ординату на епюрі М p.
Визначити кут повороту точки С балки, затисненої лівим кінцем і навантаженої рівномірно розподіленим навантаженням q (рис. 6.6).
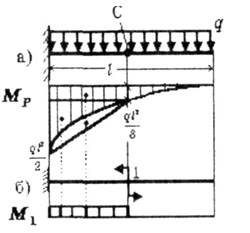
Для заданої балки із суцільною рівномірно розподіленим навантаженням інтенсивністю q визначити прогин в перерізі С. (рис. 6.7).
У багатьох випадках виявляється зручним будувати вантажну епюру в так званому "розшарованому" вигляді: будують ряд самостійних епюр від кожної навантаження. Сутність розшарування епюр покажемо на конкретному прикладі (рис. 6.7.).