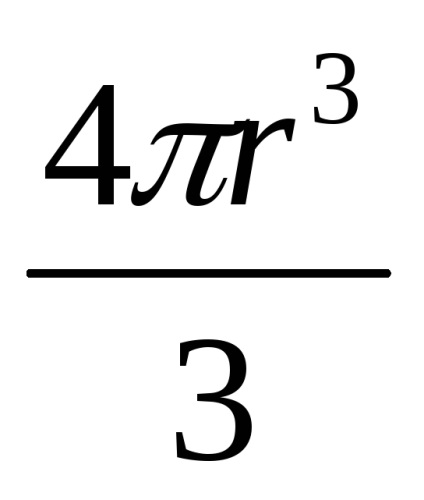сили тертя

Класифікуючи сили тертя, перш за все, поділяють сухе і в'язке тертя (рис. 3.6) .Первое виникає між сухими твердими поверхнями тіл, а друге - при русі у в'язкому середовищі, або при відносному русі тіл, розділених мастильним шаром.

При сухому терті, в свою чергу, розрізняють тертя спокою і тертя ковзання.

сухе тертя

Докладемо «невелику» силу до тіла, який лежить на горизонтальній поверхні. «Невелику» - тобто, недостатню для початку руху. Тіло буде залишатися в спокої, тому що крім доданої нами сили

сили тертя
на тіло буде діяти рівна і протилежно спрямована сила тертя. Це і є «сила тертя спокою» (рис. 3.7). Тіло буде залишатися в спокої при зміні напрямку прикладеної сили
сили тертя
і, в певних межах, її величини. Це означає, що зі зміною сили
сили тертя
буде змінюватися величина і напрямок сили тертя спокою.

Збільшуючи прикладена зусилля

сили тертя
, ми будемо спостерігати зростання сили тертя спокою. Однак, це зростання не безмежний. Коли сила тертя спокою досягне свого граничного значення
сили тертя
, почнеться ковзання тіла по поверхні. Максимальна сила тертя спокою
сили тертя
залежить від матеріалу контактуючих поверхонь, якості їх обробки і від величини сили, що притискує тіло до поверхні - сили нормального давленіяN.

сили тертя

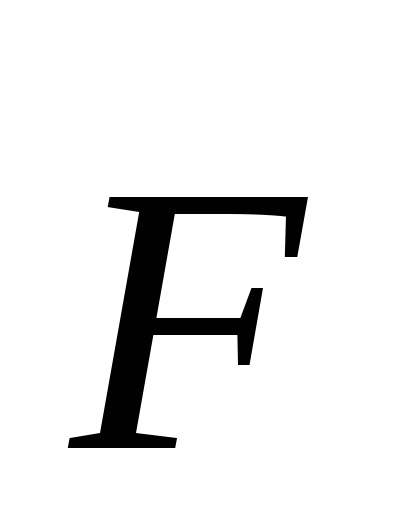
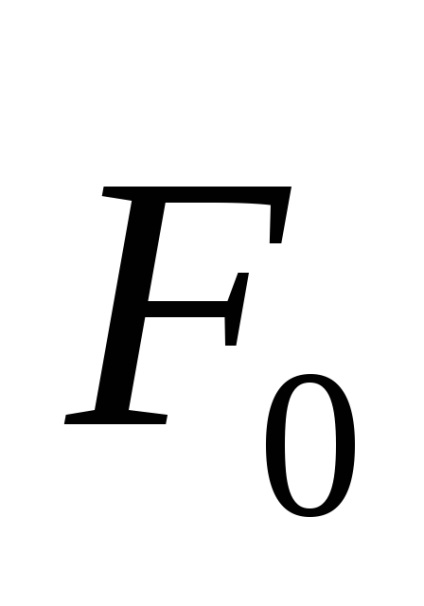
Якщо прикладена сила F превишаетF0. тіло буде рухатися з прискоренням, пропорційним рівнодіюча сілиF і сили тертя - тепер уже ковзання -Fтр.

Згідно досвідченому закону Амонтона (1699) максимальне значення сили тертя спокою F0 і сила тертя ковзання

сили тертя
пропорційні величині сили нормального тиску, що притискає тертьові поверхні один до другуN:

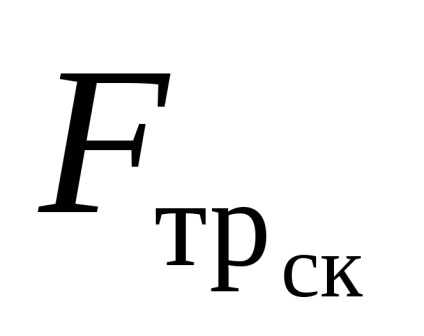
Тут - коефіцієнт сухого тертя. Це таблична величина, пов'язана як уже зазначалося, з матеріалом, що труться і якістю їх обробки.

Сила тертя ковзання не залежить від площі поверхні зіткнення тіл.

в'язке тертя

Сила в'язкого тертя діє на тіло, що рухається у в'язкому середовищі (рідкому або газоподібному). Вона залежить від форми і розмірів тіла, швидкості його руху, а також від фізичних властивостей середовища: зокрема - від щільності і вязкості.

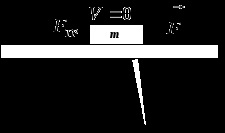
Ньютон експериментально досліджував силу в'язкого тертя, що виникає при відносному ковзанні двох поверхонь I і II, розділених шаром рідини (рис. 8).

Ця сила виявилася пропорційною швидкості V рухомий пластини I, її площадіS і обернено пропорційною толщінеh розділового шару рідини:

Тут - в'язкість рідини, [Пас].

У 1851 році англійський фізик Джордж Стокс розрахував силу в'язкого опору, що діє на твердий куля радіуса r при його повільному поступальному русі в необмеженої в'язкому середовищі:

Ця формула відома як закон Стокса.

Покажемо, як, використовуючи цей закон, можна експериментально визначити в'язкість рідини .

На кулю радіуса r. падаючий в в'язкому середовищі будуть діяти три сили (рис. 9): сила тяжестіP = тgV. сила в'язкого сопротівленіяFв.тр. = 6rv і сила гідростатичного виштовхування (Архімеда) FАрх. = жgV. тут

сили тертя
- об'єм кулі.

сили тертя

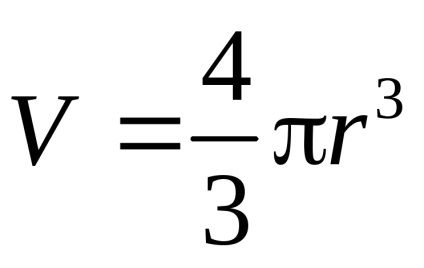
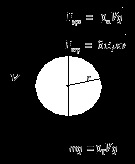
Під дією цих сил рух кулі буде відбуватися з прискоренням:

.

Важливо помітити, що в чисельнику цього виразу перші два доданків залишаються постійними, а третє в процесі руху збільшується в міру зростання швидкості кулі v.

При цьому прискорення буде зменшуватися і стане рівним нулю, коли рівнодіюча сил (чисельник) звернеться в нуль:

Далі рух буде відбуватися з постійною швидкістю v0.

Вирішимо останнє рівняння щодо коефіцієнта в'язкості :

Для обчислення в'язкості рідини нужно ізмерітьт іж - щільність речовини кулі і рідини; r іv0 - радіус кулі і швидкість його рівномірного падіння в середовищі. Звичайно, доведеться обчислити і обсяг шараV =

сили тертя
. Ця проста методика вимірювання в'язкості і сьогодні широко використовується в «віскозиметрах Стокса».

Схожі статті