Сила гідростатичного тиску на плоску стінку дорівнює добутку тиску в центрі ваги змоченої плоскої стінки, помноженому на її площа S
де hc - глибина занурення центра ваги плоскої стінки, м.
Координата прикладання сили, що діє на плоску стінку
де Jo - момент інерції плоскої фігури відносно центральної осі.
Силу тиску на криволінійну поверхню визначають як:
.
- проекція криволінійної поверхні на вертикальну площину.
де - обсяг тіла тиску, обмежений зверху площиною вільної поверхні, з боків - вертикальної проецирующей поверхнею, знизу - криволінійною поверхнею.
При вирішенні завдань з даної теми:
- на першому етапі визначають величину рівнодійної сили;
- на другому етапі визначають точку прикладення і направлення дії цієї сили.
У тому випадку, коли хоча б по одну сторону від даної поверхні тиск над вільною поверхнею рідини відмінно від атмосферного, необхідно використовувати в розрахунках повне гідростатичний тиск в центрі ваги розглянутої поверхні.
Приклад 1. Прямокутний поворотний щит розміром L 'B = 3'4 м закриває випускний отвір греблі (рис. 2.2). У лівій частині рівень води дорівнює Н2 = 2 м, в правій частині - Н1 = 5 м. Визначити силу Т натягу тросів, необхідну для відкриття щита, розташованих під кутом a до горизонту, і силу Fa. з якої щит притискається до порогу А.
Рішення. Визначимо силу, що діє на ліву частину щита.
Площа змоченої поверхні: м 2.
Глибина занурення центра ваги: м.
Сила тиску: кН.
Площа змоченою справа поверхні щита: м 2.
Глибина занурення центра ваги: м.
У цій темі необхідно засвоїти, що рівняння Бернуллі є рівнянням збереження механічної енергії потоку, віднесеної до одного кілограму ваги рідини і визначається по відношенню до загальної площини порівняння.
Механічна енергія потоку в лівій частині рівняння завжди більше такої в правій її частині на величину втрат hпот.
Рух рідини від перетину 1 до перетину 2 визначається рівнянням Бернуллі у вигляді:
тут Z1. Z2 - геометричний напір, що дорівнює відстані від живого перетину потоку до площини порівняння;
. - п'єзометричний натиск, рівний показнику пьезометра в обраному перетині.
Примітка: Значення тисків, що підставляються в рівняння повинні відраховуватися від одного рівня тисків. Або обидва надлишкові, або обидва абсолютні.
. - швидкісний напір, що враховує кінетичну енергію потоку.
a1. a2 - коефіцієнти Каріоліса, що враховують відношення дійсної кінетичної енергії потоку до енергії, розрахованої від середньої швидкості потоку.
Для ламінарного режиму a = 2. Для турбулентного a = 1,03-1,18.
- втрати механічної енергії при русі рідини. Необхідно враховувати той факт, що при русі ідеальної рідини втрати напору = 0. У всіх інших випадках їх необхідно враховувати як суму. де
- втрати на тертя. (2.10)
- втрати на місцевих опорах. (2.11)
Положення цієї площини порівняння необхідно вибирати таким чином, щоб зменшити число невідомих в рівнянні Бернуллі.
Рівняння записують у формі (2.9), потім з урахуванням положення площини порівняння і координат перетинів записують в спрощеному вигляді при цьому складові, якими нехтують, повинні бути обгрунтовані.
При визначенні швидкісних напорів в кожному перетині необхідно використовувати рівняння суцільності (сталості витрати в каналі)
Студент самостійно перевіряє побудова ліній повного і п'єзометричного напору по специфічними перетинах з урахуванням даних. Наприклад, лінія повного напору в перерізі на вільної поверхні рідини в баку збігається з лінією п'єзометричного напору, тому що V = 0.
Якщо тиск над вільною поверхнею більше атмосферного, то лінія повного напору пройде вище рівня рідини і т.д.
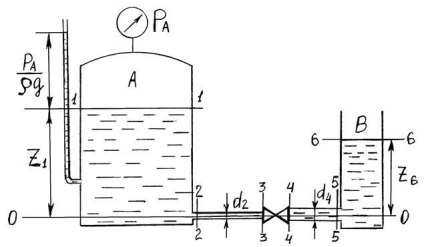
Приклад. Трубопровід, що складається з труб різних діаметрів мм і мм, з'єднує ресивер А з атмосферним баком В. Рівень рідини в ресівері м, тиск над поверхнею рідини атм. Визначити рівень в баку В при витраті рідини Q. рівному 1 л / с. Втрати напору при цьому складають: на виході в трубопровід м; на першій ділянці h3 = 2 м; на вентилі, що розділяє трубопровід, h4 = 2 м; на другій ділянці h5 = 5 м (рис. 2.4).
Рішення. Вибираємо площину порівняння, що проходить через вісь трубопроводу, запишемо рівняння Бернуллі для двох перерізів, що проходять через площині вільного рівня в ресівері 1-1 і в атмосферному баку 6-6.
де - сумарні втрати напору від перетину 1-1 до перетину 6-6.
. Для кожного перетину розраховуються швидкість. число Рейнольдса. уточнюється коефіцієнт Каріоліса.