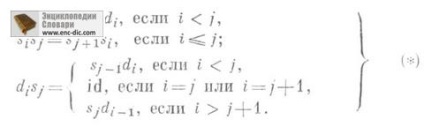
Точки шару До п зв. n-мірними симплекс С. м. К. Якщо задані тільки оператори di. задовольняють співвідношенням di dj = dj-1 di. i
Симпліціального відображенням f: До К 'С. м. Кв С. м. К' зв. морфізм функторів, т. е. послідовність відображень,, що задовольняють співвідношенням,
Для будь-якого топологіч. простору Xопределено С. м. S (X), наз. сингулярним С. м. простору X, симплекс догрого є сингулярні симплекси простору X (див. Сингулярні гомології), т. е. безперервні відображення. де D n - n-мірний геометричний стандартний симплекс
Оператори граней di і виродження si цього С. м. Визначаються формулами
С. м. К (p) є насправді симпліціального групою.
Для довільної абельовой групи p і будь-якого цілого визначено С. м. (Насправді, симпліціального абелева група) E (p, п), симплекс розмірності qк-якого є re-мірні коцепі q-мірного геометричного стандартного симплекса D q з коефіцієнтами в групі я (таким чином, Е (p, n) q = С n (D q; p)). Позначаючи вершини симплекса D q символами, визначають симпліціального відображення і формулами
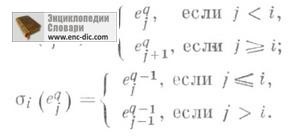
Індуковані гомоморфізм груп коцепей
є, за визначенням, операторами граней і виродження С. м. Е (p, п). Симплекси, є коцікламі, утворюють симпліціального підмножина С. м. Е (p, п), до-рої зв. С. м. Ейленберга - Маклейна і позначається К (p, n). Прикордонний оператор на групах С * (D q; p) визначає канонічне симпліціального відображення Е (p, п) K (p, n +1), до-рої позначається d. Оскільки поняття одновимірного коцікла має сенс і для неабелева групи p (див. Неабелева когомологий), С. м. К (p, 1) визначено і без припущення, що група p абелева. Це С. м. + (К) .ізоморфни і зв. групами (до) гомологий симпліціального схеми К. Групи (ко) гомологий С. м. К (p) суть групи (до) гомологий групи p.
Симплекс С. м. Кназ. виродженим, якщо існує такий симплекс і такий оператор виродження si, що х = si у. Лемма Ейленберга - Зильбера стверджує, що будь-який симплекс С. м. Кедінственним чином представляється у вигляді x = K (s) y, де s- недо-рий епіморфізм, а - невироджених симплекс. Найменша симпліціального підмножина С. м. К, що містить всі його невироджені симплекси розмірності, меншою або рівною n, позначається До n або Sk n K і зв. n-мірним остовом С. м. К.
Геометричні стандартні симплекси
складають косімпліціальное топологіч. простір щодо операторів кограней di і ковирожденія si. визначених формулами
У діз'юнктном об'єднанні, де все До n розглядаються як дискретні безлічі, формули
визначають ставлення еквівалентності, факторпространством по до-рому є клітинним розбиттям (клітинним простором), клітини догрого знаходяться в биективное відповідно до невиродженими cімплексамі С. м. К. Це клітинне розбиття позначається | До | або RK і зв. геометричній реалізацією в сенсі Мілнора С. м. К. Кожне симпліціального відображення індукує по формулі
безперервне відображення, і відповідності є функтор R :. Цей функтор пов'язаний зліва до сингулярного функтором. Відповідні ізоморфізми функторів
Морфізм сполучення є для будь-якого топологіч. простору Xслабой гомотопіч. еквівалентністю (це, зокрема, доводить, що довільне топологіч. простір слабо гомотопічно еквівалентно клітинному розбиття).
Конструкція геометричний. реалізації | До | узагальнюється на сімшшціальние топологіч. простору К. Можна. також визначити геометричну реалізацію в сенсі Джівера - Ху || K ||, що враховує тільки оператори граней di (в цій реалізації є клітини для всіх симплексів з К, а не тільки невироджених). Якщо кожен оператор виродження si є замкнутим корасслоеніем (умова, автоматично виконане для С. м.), То природне відображення є гомотопіч. еквівалентність.
Зокрема, для кожного С. м. Копределено його твір на симпліціального відрізок D 1. Проекції і визначають биективное відображення
доорої є гомеоморфізмом, коли твір RK X RL являє собою клітинне розбиття (напр. якщо обидва С. м. Ки Lсчетни або ж якщо одне з клітинних розбиття RK або RL локально звичайно). Звідси, зокрема, випливає, що геометричний. реалізація будь-якого рахункового симпліціального моноїд (групи, абельовой групи) є топологіч. моноїд (групою, абельовой групою).
Симпліціального відображення зв. гомотопних, якщо існує таке симпліціального відображення (гомотопия) L, що
для будь-якого симплекса і для будь-якої композиції s (довжини п) .операторов виродження. Це визначення (моделює звичайне визначення гомотопії неперервних відображень) рівносильно (для випадку С. м.) Загальним визначенням гомотопних симпліціального відображень будь-яких симпліціального об'єктів.
Симпліціального відображення стандартного кулька (див. Стандартний симплекс) .в С. м. Кназ. кульком в К. Кожен кульок однозначно задається (n + 1) - членной послідовністю n-мірних симплексів х 0. x1. xk-1. xk + 1. xn + 1 для яких брало di xj = dj-1 xi при будь-яких. Кажуть, що Фунтик заповнюється, якщо він поширюється на всі С. м. D n + 1. т. е. знайдеться такий (n + 1) -мірний симплекс х, що di x = xi для кожного. С. м. Кназ. повним (або задовольняє умові Кана), якщо кожен його Фунтик заповнюється.
сопоставляющий кожному С. м. Кполное С. м., геометричний. реалізація догрого гомотоніческі еквівалентна геометричний. реалізації С. м. Ки доорої тому цілком замінює С. м. Кво всіх гомотопічних питаннях.
Два n-мірних симплекса хі х 'С. м. Кназ. порівнянними, якщо. Порівнянні симплекси зв. гомотопних, якщо існує такий (n + 1) -мірний симплекс у, що dn y = x, dn + 1 y = x 'і di y = sn-1 di x = sn-1 di x'. . Для повних С. м. Цей показник є відношенням еквівалентності, причому симплекси тоді і тільки тоді гомотопних, коли їх характеристичні симпліціального відображення гомотопних.
С. м. Кназ. пунктіровать, якщо в ньому відзначено недо-рий нульмерние симплекс q (тим же символом q позначаються всі виродження цього симплекса, а також породжене їм симпліціального підмножина, до-рої зазвичай зв. зазначеної точкою в К). Для повного пунктіровать С. м. Кмножество Рп (К) .классов гомотопних га-мірних симплексів, порівнянних з симплексом q, є при групою. Ця група зв. n-м ерной гомотопічній групою пунктіровать повного С. м. К; ця термінологія виправдовується тим, що pn (К) .pп (| До |), і зокрема pn (К (p, n)) = p і pi (K (p, п)). = 0 при. С. м. К, для к-якого pi (К) .0 при всіх, наз. n-зв'язковим; при цьому 0-зв'язний С. м. зв. зв'язковим, а 1-зв'язний С. м.- однозв'язного. Додавання в групі, індукується операцією, сопоставляющей симплекс хі у (можна порівняти з q) симплекс dn z, де z - симплекс розмірності n + 1, що заповнює кульок xi = 0,, х n-1 = х, х п + 1 = у. Якщо С. м. Кявляется симпліціального моноїд з одиницею q, то складання індукується також множенням в цьому моноїд (твір двох симплексів, порівнянних з q, можна порівняти з q).
Оскільки будь-який симплекс у, який можна порівняти з q, є циклом (ланцюгового комплексу С (К), що визначається С. м. К), то виникає природне гомоморфізм
Гуревича, при п = 1 индуцирующий ізоморфізм
(Теорема Пуанкаре), а при n> 1 є изоморфизмом, коли С. м. К (п-1) -связно (теорема Гуревича). Для повних С. м. Справедлива також і теорема Уайтхеда в обох її варіантах, т. Е. Симпліціального відображення повних С. м. Тоді і тільки тоді є гомотопіч. еквівалентність, коли воно індукує ізоморфізм гомотопіч. груп, причому для однозв''язних С. м. ця умова рівнозначно тому, що індуковані гомоморфізм груп гомології є ізоморфізм.
У разі, коли Кявляется симпліціального групою, гомотопіч. група pn (К) .ізоморфна групі гомології ланцюгового (не обов'язково абелева) комплексу, для к-якого