Синус, косинус, тангенс що таке як знайти синус, косинус і тангенс

Одним з розділів математики, з якими школярі справляються з найбільшими труднощами, є тригонометрія. Не дивно: для того щоб вільно оволодіти цією областю знань, потрібна наявність просторового мислення, вміння знаходити синуси, косинуси, тангенси, котангенс за формулами, спрощувати вирази, вміти застосовувати в обчисленнях число пі. Крім цього, потрібно вміти застосовувати тригонометрію при доказі теорем, а це вимагає або розвиненою математичної пам'яті, або вміння виводити непрості логічні ланцюжки.

витоки тригонометрії

Знайомство з цією наукою слід почати з визначення синуса, косинуса і тангенса кута, однак спочатку необхідно розібратися, чим взагалі займається тригонометрія.

Історично головним об'єктом дослідження даного розділу математичної науки були прямокутні трикутники. Наявність кута в 90 градусів дає можливість здійснювати різні операції, що дозволяють по двох сторонах і одному кутку або по двох кутах і одній стороні визначати значення всіх параметрів даної фігури. У минулому люди помітили цю закономірність і стали активно нею користуватися при будівництві будівель, навігації, в астрономії і навіть в мистецтві.

Початковий етап

Спочатку люди міркували про взаємовідносини кутів і сторін виключно на прикладі прямокутних трикутників. Потім були відкриті особливі формули, що дозволили розширити кордони вживання в повсякденному житті даного розділу математики.

Вивчення тригонометрії в школі сьогодні починається з прямокутних трикутників, після чого отримані знання використовуються учнями у фізиці і вирішенні абстрактних тригонометричних рівнянь, робота з якими починається в старших класах.

сферична тригонометрія

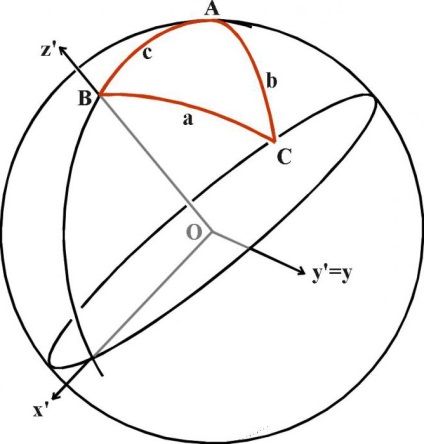
Пізніше, коли наука вийшла на наступний рівень розвитку, формули з синусом, косинусом, тангенсом, котангенсом стали використовуватися в сферичної геометрії, де діють інші правила, а сума кутів в трикутнику завжди більше 180 градусів. Даний розділ не вивчається в школі, проте знати про його існування необхідно як мінімум тому, що земна поверхня, та й поверхню будь-якої іншої планети, є опуклою, а значить, будь-яка розмітка поверхні буде в тривимірному просторі «дугоподібної».

Візьміть глобус і нитку. Прикладіть нитку до двох будь-яким точкам на глобусі, щоб вона виявилася натягнутій. Зверніть увагу - вона знайшла форму дуги. З такими формами і має справу сферична геометрія, що застосовується в геодезії, астрономії та інших теоретичних і прикладних областях.

Прямокутний трикутник

Трохи дізнавшись про способи застосування тригонометрії, повернемося до базової тригонометрії, щоб в подальшому розібратися, що таке синус, косинус, тангенс, які розрахунки можна з їх допомогою виконувати і які формули при цьому використовувати.

Насамперед необхідно усвідомити поняття, які стосуються прямокутного трикутника. По-перше, гіпотенуза - це сторона, що лежить навпроти кута в 90 градусів. Вона є найдовшою. Ми пам'ятаємо, що по теоремі Піфагора її чисельне значення дорівнює кореню з суми квадратів двох інших сторін.

Наприклад, якщо дві сторони рівні 3 і 4 сантиметрам відповідно, довжина гіпотенузи складе 5 сантиметрів. До речі, про це знали ще стародавні єгиптяни близько чотирьох з половиною тисяч років тому.

Дві що залишилися боку, які утворюють прямий кут, звуться катетів. Крім того, треба пам'ятати, що сума кутів в трикутнику в прямокутній системі координат дорівнює 180 градусам.

визначення

Нарешті, твердо розуміючи геометричну базу, можна звернутися до визначення синуса, косинуса і тангенса кута.

Синусом кута називається відношення протилежного катета (т. Е. Сторони, що розташовується навпроти потрібного кута) до гіпотенузи. Косинусом кута називається відношення прилеглого катета до гіпотенузи.

Запам'ятайте, що ні синус, ні косинус не може бути більше одиниці! Чому? Тому що гіпотенуза - це за замовчуванням найдовша сторона прямокутного трикутника. Яким би довгим не був катет, він буде коротше гіпотенузи, а значить, їх ставлення завжди буде менше одиниці. Таким чином, якщо у вас у відповіді до задачі вийшов синус або косинус зі значенням, більшим, ніж 1, шукайте помилку в розрахунках або міркуваннях. Ця відповідь однозначно невірний.

Нарешті, тангенсом кута називається відношення противолежащей боку до прилеглої. Той же самий результат дасть розподіл синуса на косинус. Подивіться: відповідно до формули ми ділимо довжину сторони на гіпотенузу, після чого ділимо на довжину другої сторони і множимо на гіпотенузу. Таким чином, ми отримуємо те ж саме співвідношення, що і у визначенні тангенса.

Котангенс, відповідно, являє собою відношення прилеглої до кута сторони до протилежної. Той же результат ми отримаємо, розділивши одиницю на тангенс.

Отже, ми розглянули визначення, що таке синус, косинус, тангенс і котангенс, і можемо зайнятися формулами.

найпростіші формули

У тригонометрії не обійтися без формул - як знайти синус, косинус, тангенс, котангенс без них? А адже саме це потрібно при вирішенні завдань.

Перша формула, яку необхідно знати, починаючи вивчати тригонометрію, говорить про те, що сума квадратів синуса і косинуса кута дорівнює одиниці. Дана формула є прямим наслідком теореми Піфагора, проте дозволяє заощадити час, якщо потрібно дізнатися величину кута, а не сторони.

Багато учні не можуть запам'ятати другу формулу, також дуже популярну при вирішенні шкільних завдань: сума одиниці і квадрата тангенса кута дорівнює одиниці, поділеній на квадрат косинуса кута. Придивіться: адже це те ж саме твердження, що і в першій формулі, тільки обидві сторони тотожності були поділені на квадрат косинуса. Виходить, проста математична операція робить тригонометричну формулу абсолютно невпізнанною. Пам'ятайте: знаючи, що таке синус, косинус, тангенс і котангенс, правила перетворення і кілька базових формул ви в будь-який момент зможете самі вивести необхідні більш складні формули на аркуші паперу.

Формули подвійного кута і складання аргументів

Ще дві формули, які потрібно вивчити, пов'язані зі значеннями синуса і косинуса при сумі і різниці кутів. Вони представлені на малюнку нижче. Зверніть увагу, що в першому випадку обидва рази перемножується синус і косинус, а в другому складається попарне твір синуса і косинуса.

Також існують формули, пов'язані з аргументами у вигляді подвійного кута. Вони повністю виводяться з попередніх - в якості тренування спробуйте отримати їх самостійно, прийнявши кут альфа рівним куту бета.

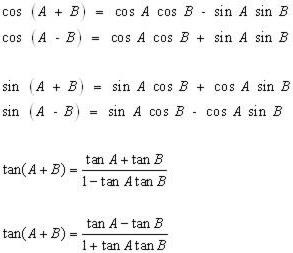
Нарешті, зверніть увагу, що формули подвійного кута можна перетворити так, щоб знизити ступінь синуса, косинуса, тангенса альфа.

Двома основними теоремами в базовій тригонометрії є теорема синусів і теорема косинусів. За допомогою цих теорем ви легко зможете зрозуміти, як знайти синус, косинус і тангенс, а значить, і площа фігури, і величину кожного боку і т. Д.

Теорема синусів стверджує, що в результаті поділу довжини кожної зі сторін трикутника на величину протилежного кута ми отримаємо однакове число. Більш того, це число буде дорівнює двом радіусів описаного кола, т. Е. Окружності, що містить всі точки даного трикутника.

Теорема косинусів узагальнює теорему Піфагора, проектуючи її на будь-які трикутники. Виявляється, з суми квадратів двох сторін відняти їх твір, помножене на подвійний косинус суміжного їм кута - отримане значення виявиться дорівнює квадрату третьої сторони. Таким чином, теорема Піфагора виявляється окремим випадком теореми косинусів.

Помилки через неуважність

Навіть знаючи, що таке синус, косинус і тангенс, легко зробити помилку через неуважність уваги або помилки в найпростіших розрахунках. Щоб уникнути таких помилок, ознайомимося з найбільш популярними з них.

Далі, зверніть увагу, що до будь-якого трикутника може бути застосована теорема косинусів, але не теорема Піфагора! Якщо ви помилково забудете відняти подвоєний добуток сторін, помножене на косинус кута між ними, ви не тільки отримаєте абсолютно невірний результат, а й продемонструєте повне нерозуміння предмета. Це гірше, ніж помилка через неуважність.

По-третє, не плутайте значення для кутів в 30 і 60 градусів для синусів, косинусів, тангенсів, котангенсів. Запам'ятайте ці значення, адже синус 30 градусів дорівнює косинусу 60, і навпаки. Їх легко переплутати, внаслідок чого ви неминуче отримаєте помилковий результат.

застосування

Багато учнів не поспішають приступати до вивчення тригонометрії, оскільки не розуміють її прикладного сенсу. Що таке синус, косинус, тангенс для інженера або астронома? Це поняття, завдяки яким можна обчислити відстань до далеких зірок, передбачити падіння метеорита, відправити дослідницький зонд на іншу планету. Без них не можна побудувати будинок, спроектувати автомобіль, розрахувати навантаження на поверхню або траєкторію руху предмета. І це тільки найочевидніші приклади! Адже тригонометрія в тому чи іншому вигляді використовується всюди, починаючи від музики і закінчуючи медициною.

На закінчення

Отже, ви знаєте, що таке синус, косинус, тангенс. Ви можете використовувати їх в розрахунках і успішно вирішувати шкільні завдання.

Вся суть тригонометрії зводиться до того, що за відомими параметрами трикутника потрібно обчислити невідомі. Всього цих параметрів шість: довжини трьох сторін і величини трьох кутів. Все відмінність в задачах полягає в тому, що даються неоднакові вхідні дані.

Як знайти синус, косинус, тангенс виходячи з відомих довжин катетів або гіпотенузи, ви тепер знаєте. Оскільки ці терміни позначають не що інше, як відношення, а відношення - це дріб, головною метою тригонометричної завдання стає знаходження коренів звичайного рівняння або ж системи рівнянь. І тут вам допоможе звичайна шкільна математика.

Схожі статті

• Як знайти тангенс через косинус