При роботі з тривимірною графікою використовується кілька видів систем координат. Для відображення двовимірних об'єктів нам була потрібна відповідна система координат з двома осями - горизонтальною віссю X і вертикальною віссю Y. Нагадаємо, що екранна система координат для двовимірної графіки має початок (точку 0,0) в лівому верхньому кутку монітора, позитивна частина осі X розташовується праворуч від початку координат, позитивна частина осі Y - знизу.
Для роботи з тривимірними об'єктами нам знадобиться ще одна вісь - вона називається вісь Z. Існує кілька варіантів тривимірних систем координат, зокрема, поширені так звані правобічна і лівостороння системи. Ми будемо користуватися правобічної системою - вона застосовується в XNA Framework. Її схематичне зображення наведено на рис. 1.
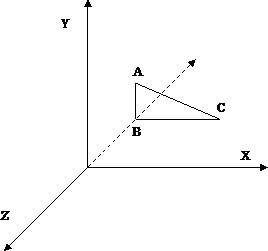
Мал. 1. Правосторонняя система координат
Особливість цієї системи координат полягає в тому, що початок координат можна зіставити з лівим нижнім кутом монітора, позитивна частина осі X знаходиться праворуч від початку координат, позитивна частина осі Y - зверху, а позитивна частина осі Z - спереду. А це означає, що видима частина осі Z - це її негативна частина. Ця частина осі перебуває ніби «в глибині монітора», в той час, як позитивна частина знаходиться «попереду монітора». На рис. 1. пунктиром зображена негативна частина осі Z.
У двовимірної системі координат існує поняття точки - її координати задаються двома значеннями - X і Y. Точки існують і в тривимірній системі координат - вони задаються вже трьома значеннями - X, Y, Z.
Точки використовують для того, щоб ставити координати вершин багатокутників (полігонів), зокрема - трикутників. Так, трикутник, зображений на рис. 1. заданий трьома крапками - A, B, C.
Як правило, більш складні тривимірні об'єкти будуються саме з трикутників.
У тривимірній графіці існує таке поняття, як грань (face). Це - плоский об'єкт, який визначають кілька вершин. У нашому випадку звичайний трикутник - це саме грань. З кількох плоских граней можна зібрати об'ємний об'єкт.
Чим більше трикутників використано при побудові моделі - тим більше деталізованої вона виходить. Точки, що відповідають вершинам трикутника, який можна зобразити у тривимірному просторі, називаються вершинами. Можливо, вам зустрінеться множину слова вершина: «вершини» виглядає по-англійськи як «vertices». Іноді для позначення вершин використовують кальку з англійської - вертекс.
Трикутник не випадково була обрана в якості базової геометричної фігури - по-перше - цей багатокутник завжди є опуклим, по-друге - неможливо розташувати три точки таким чином, щоб вони не належали одній площині. Тобто, трикутник - це фігура, яка завжди є опуклою і плоскою, що дозволяє з успіхом використовувати його в цілях тривимірної графіки.
Кілька граней, з яких складається тривимірний об'єкт, називаються сіткою (mesh). "Сітка" являє собою набір трикутників.
Ще одне поняття, яке стане в нагоді вам при роботі з тривимірною графікою - це поняття вектора. Вектор (vector), так само як і точка, може бути визначений трьома параметрами, однак він описує не положення в просторі, а напрямок і швидкість руху.
Вектор має початок і кінець, для його повного визначення потрібно знати координати точки початку і кінця вектора, тобто, замість трьох значень координат нам знадобиться вже шість значень. Однак, якщо за замовчуванням прийняти за початок вектора початок координат (точку 0,0,0) - тоді для його визначення вистачить і трьох точок.
Наприклад, вектор з координатами (1,0,0) означає: «напрямок - вправо, швидкість - 1». Якщо відкласти цей вектор від початку координат, то добре видно, що він спрямований саме вправо (рис. 2.).
Напрямок вектора визначається положенням другої точки щодо першої (в нашому випадку - положення точки кінця вектора, якої задається вектор щодо початку координат), а швидкість - довжиною вектора - тобто - різницею між початковою і кінцевою точкою. У нашому випадку довжина вектора збігається з координатами його кінця.
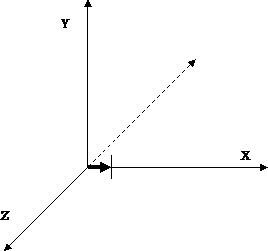
Мал. 2. Вектор (1,0,0)
Існує особливий вид векторів - нормалі (normals). Нормалі можуть бути побудовані для граней і для вершин об'єкта. Нормалі для граней перпендикулярні цим гранях. Вони використовуються при розрахунку кольору об'єкта.