Величина дробу не зміниться, якщо чисельник і знаменник дробу помножити на одне і те ж число.
= =;
= =;
= =;
Таке перетворення дробу називається «розширенням» дробу. Дріб отримана розширенням на 6 з дробу.
Величина дробу не зміниться, якщо чисельник і знаменник дробу розділити на одне і теж число.
Таке перетворення називається скороченням дробу.
Слово «відсоток» походить від латинського «procento», що означає «з сотні».
Відсоток - це сота частина числа, позначається знаком%.
Будь-яке ціле число (наприклад 1) становить 100%. Його сота частина 1. 100 = 0,01. Отже, 1% від одиниці складе 0,01.
Якщо в задачі величина в цілому невідома, а відомі лише її частини, то вона приймається за 100% або за 1 (одиницю). Коли ціле складається з яких - то частин, то ці частини складають дроби, сума яких дорівнює цілому (1). Пропорційно цим дробям частина цілого можна взяти і в процентах.
Якщо весь обсяг - 100%, то кожна частина (кожна дріб) становить величину більше 0%, але менше 100%, а сума всіх частин у відсотках дорівнює 100%. Відсоток який - то величини - це частина (частка) цієї ж величини, тому, якщо 1 = 100%, то і кожна дріб (звичайна або десяткова) дорівнює якого - то відсотку від 1.
Приклад: округлятимете до тисячних число 0,3442524.
Тисячні - це третій розряд після коми, значить, нам треба дивитися на четвертий цифру:
0,3442 524 - в даному випадку це 2, тому округляем в меншу сторону і отримуємо 0,344.
Нагадаємо, що при цифрах 0,1,2,3,4 округляем в меншу сторону. При цифрах 5,6,7,8,9 округляємо в більшу сторону. Таким чином у нас є п'ять випадком і в округленні в меншу і більшу сторону.
текстові завдання # 8213; це одні з найменш улюблених завдань, особливо в учнів старших класів, тому що чим далі, тим заплутаніше стає умова, тим складніше стає скласти рівняння і правильно вирішити задачу. Але, як і в будь-якій темі в математиці, щоб впевнено вирішувати складні завдання, необхідно розібратися з самими основними прийомами.
Розберемо ці завдання з самого початку. Текстова завдання складається з умови, в якому описана деяка ситуація, і питання, на який потрібно дати відповідь.
Приклад: Коля наклеїв на 5 аркушів по 2 наклейки. Скільки наклейок наклеїв Коля?
Умова: Коля наклеїв на 5 аркушів по 2 наклейки.
Питання: Скільки наклейок наклеїв Коля?
Рішення будь-якої текстової задачі можна розділити на кілька основних етапів:
· Робота з умовою;
· Для одного рівняння може бути складено безліч різних умов.
Умова 1: Маша і Петя разом знайшли 5 грибів. Маша знайшла 2. Скільки грибів знайшов Петя?
Умова 2: Букет складається з ромашок і дзвіночків. Всього в букеті 5 квіток, з них 2 ромашки. Скільки дзвіночків в букеті?
Умова 3: На ялинці було 5 іграшок. Дві з них впали і розбилися. Скільки іграшок залишилося на ялинці?
Для полегшення роботи з умовою корисно використовувати ілюстрацію або моделювання. Це може бути короткий запис умови математично або словесно. Також це може бути додатковий малюнок або таблиця.
Приклад: Петя вище Колі, Сергій нижче Колі. Хто вище?
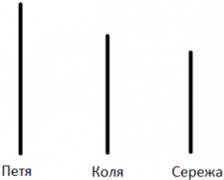
З малюнка відразу зрозуміла відповідь: Петя вище всіх.
Для складання рівняння за умовою задачі використовуються різні прийоми, залежно від даної в умові залежності величин.
Така залежність виражається в словах: вище / нижче, більше / менше, дорожче / дешевше, довше / коротше і т. Д.
При складанні рівняння особливе значення відіграють використовувані приводи: «в» і «на».
Приклад: Петя вище Колі на 20 см, Сергій нижче Колі на 10 см. На скільки см Петя вище Сергія?
Рішення: Нехай П # 8213; зростання Петі, К # 8213; зростання Колі, С # 8213; зростання Сергія.
До речі, зверніть увагу на цей прийом # 8213; вибирати «говорять» змінні, а не безликі ікси і ігреки, щоб не заплутатися при роботі з рівнянням.
Висловимо зростання хлопчиків.
Петя вище Колі на 20 см: П - 20 = К.
Сергій нижче Колі на 10 см: К = С + 10.
Підставами до першого рівняння зростання Колі: П - 20 = С + 10.
Нам потрібно знайти, на скільки см Петя вище Сергія: П - С.
Отримуємо, що Петя вище Сергія на 30 см.
Приклад: На уроці праці учні робили сніжинки. Всього було зроблено 12 сніжинок. Маша зробила в два рази більше сніжинок, ніж Коля. Коля зробив на 4 сніжинки менше, ніж Рома. Скільки сніжинок зробила Маша?
нехай М # 8213; кількість сніжинок, яке зробила Маша, К - сніжинки Колі, Р # 8213; сніжинки Роми.
Маша зробила в два рази більше сніжинок, ніж Коля: К = М / 2.
Коля зробив на 4 сніжинки менше, ніж Рома: Р = К + 4 = М / 2 + 4.
Разом хлопці зробили 12 сніжинок: М + К + Р = 12.
Підставами все виражені через М значення: М + М / 2 + М / 2 + 4 = 12.
Маша зробила 4 сніжинки.
відсоток # 8213; це завжди частка якогось числа.
100% # 8213; все число;
50% # 8213; половина;
25% # 8213; чверть.
Щоб знайти 1%, необхідно поділити все число на 100.
1% від усіх яблук # 8213; = 1 яблуко.
1% від всіх груш # 8213; = 2 груші.
Для роботи з відсотками використовується пропорція, в якій в одному стовпці записуються реальні значення, в іншому # 8213; відповідні відсотки.
200 груш # 8213; 100%;
Прогресія відображає залежність величин. По-іншому це можна записати у вигляді двох дробів: =.
Виходячи з правил роботи з дробом, отримуємо правила роботи з пропорцією:
· Всередині однієї дробу можна скорочувати значення.
· Твір навхрест лежачих значень дорівнює: 200 # 8729; 1 = 2 # 8729; 100.
Цю тему ми ще детально пройдемо на курсі.
Також текстові задачі можуть бути присвячені прогресу, продуктивності, темпу # 8213; про все це ми поговоримо на нашому курсі. А зараз приступайте до завдань для тренування.
трапеція # 8213; це чотирикутник, у якого дві протилежні сторони паралельні.
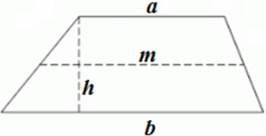
h # 8213; висота трапеції (відстань між основами);
m # 8213; середня лінія трапеції (відрізок, що з'єднує середини бічних сторін трапеції).
Середня лінія трапеції дорівнює напівсумі підстав: m = і паралельна їм:
1) Прямокутна # 8213; трапеція, що має прямі кути при бічній стороні:
· Бічна сторона є висотою.
2) рівнобедреного # 8213; трапеція, у якої бічні сторони рівні:
· Кути при підставах дорівнюють
· Довжини діагоналей рівні
· Сума внутрішніх кутів трапеції (як і будь-якого чотирикутника) дорівнює 360 °.
· Сума кутів, прилеглих до бічної сторони, дорівнює 180 °.
· У трапецію можна вписати коло, якщо сума підстав трапеції дорівнює сумі її бічних сторін.
· Якщо трапецію можна вписати в коло, то трапеція # 8213; рівнобедрена.
· Близько рівнобедреної трапеції можна описати коло.
S = m # 8729; h. де m # 8213; середня лінія трапеції.