Слідом прямої лінії називається точка (рис.17), в якій пряма перетинається з площиною проекцій (так як слід належить одній з площин проекцій то його одна координата повинна бути дорівнює нулю).
Горизонтальний слід - М (zM = 0) -точка перетину прямої з горизонтальною площиною проекцій.
Фронтальний слід - N (yN = 0) - точка перетину прямої з фронтальним площиною проекцій.
Профільний слід - Т (xТ = 0) - точка перетину прямої з профільної площиною проекцій.
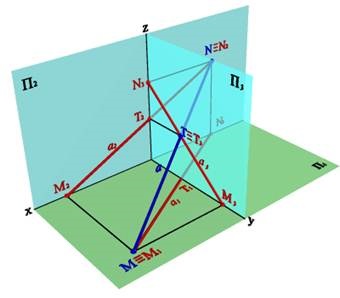
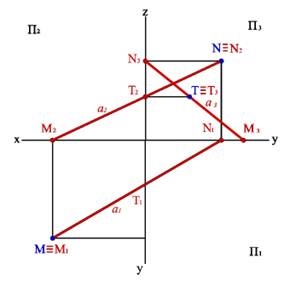
Мал. 17. Сліди прямої лінії в системі трьох площин проекцій
Сліди прямої є точками приватного положення. Однойменні проекції сліду прямої збігаються з самим слідом, а інші проекції лежать на осях. Наприклад, фронтальний слід прямої N2ºN, а N1 лежить на осі x, N3 - на осі z. Зазначені особливості в розташуванні слідів проекцій дозволяє сформулювати наступні правила:
1. Для побудови горизонтального сліду М прямий необхідно продовжити її фронтальну проекцію до перетину з віссю 0x і в цій точці відновити перпендикуляр до осі до перетину з горизонтальною проекцією прямої.
2. Для побудови фронтального сліду N прямий потрібно з точки перетину горизонтальної проекції її з віссю 0x відновити перпендикуляр до перетину з фронтальною проекцією прямої.
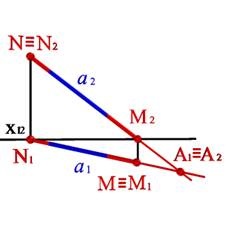
Мал. 18. Знаходження горизонтального і фронтального слідів прямої лінії
За допомогою цих правил знайдені на епюрі сліди прямої а (рис.18). Тут же показані збіглися проекції точки А що належить даної прямої.
Сліди прямої, є точками, в яких пряма переходить з одного октанта в інший, дозволяють відзначати її видимість. Видимою частиною прямої буде та, яка розташована в межах першого октанта.