"Рахунок і обчислення - основа порядку в голові".
Песталоцці
- Познайомитися зі старовинними прийомами множення.
- Розширити знання з різним прийомам множення.
- Навчитися виконувати дії з натуральними числами, використовуючи старовинні способи множення.
Актуальність використання прийомів швидкого рахунку.
У сучасному житті кожній людині часто доводиться виконувати величезну кількість розрахунків і обчислень. Тому мета моєї роботи - показати легкі, швидкі і точні методи рахунку, які не тільки допоможуть вам під час будь-яких розрахунках, але викличуть чималий подив у знайомих і товаришів, адже вільне виконання рахункових операцій в значній мірі може свідчити про непересічність вашого інтелекту. Основоположним елементом обчислювальної культури є свідомі і міцні обчислювальні навички. Проблема формування обчислювальної культури актуальна для всього шкільного курсу математики, починаючи з початкових класів, і вимагає не простого оволодіння обчислювальними навичками, а використання їх в різних ситуаціях. Володіння обчислювальними вміннями і навичками має велике значення для засвоєння матеріалу, що вивчається, дозволяє виховувати цінні трудові якості: відповідальне ставлення до своєї роботи, вміння виявляти і виправляти допущені в роботі помилки, акуратне виконання завдання, творче ставлення до праці. Однак, останнім часом рівень обчислювальних навичок, перетворень виразів має яскраво виражену тенденцію до зниження, учні допускають масу помилок при підрахунках, все частіше використовують калькулятор, не мислять раціонально, що негативно позначається на якості навчання і рівні математичних знань учнів в цілому. Однією зі складових обчислювальної культури є усний рахунок. який має велике значення. Уміння швидко і правильно зробити нескладні обчислення "в умі" необхідно для кожної людини.
Старовинні способи множення чисел.
1. Старовинний спосіб множення на 9 на пальцях
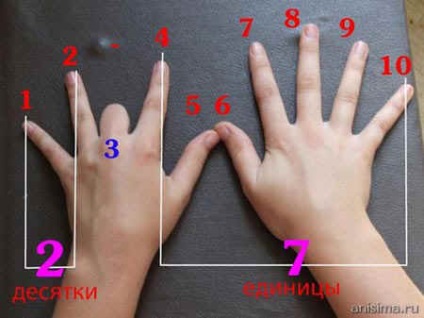
Це просто. Щоб помножити будь-яке число від 1 до 9 на 9, подивіться на руки. Загніть палець, який відповідає множити числа (наприклад 9 x 3 - загніть третій палець), порахуйте пальці до загнутого пальця (в разі 9 x 3 - це 2), потім порахуйте після загнутого пальця (в нашому випадку - 7). Відповідь - 27.
Для множення одиниць твору переумножении перемножують одиниці множників, для отримання десятків, множать десятки одного на одиниці іншої і навпаки і результати складають, для отримання сотень перемножують десятки. Методом Ферролі легко перемножать усно двозначні числа від 10 до 20.
б) 1х4 + 2х1 = 6, пишемо 6
Такий прийом нагадує множення стовпчиком, але проводиться досить довго.
Використання прийому. Припустимо, нам треба помножити 13 на 24. Накреслимо наступний малюнок:
Цей малюнок складається з 10 ліній (кількість може бути будь-яким)- Ці лінії позначають число 24 (2 лінії, відступ, 4 лінії)
- А ці лінії позначають число 13 (1 лінія, відступ, 3 лінії)
Тепер потрібно порахувати перетину ліній на всіх чотирьох кінцях наступним способом:
(Перетину на малюнку вказані точками)

- Верхній лівий край: 2
- Нижній лівий край: 6
- Верхній правий: 4
- Нижній правий: 12
1) Перетинання в верхньому лівому краї (2) - перше число відповіді
2) Сума перетинів нижнього лівого і верхнього правого країв (6 + 4) - друге число відповіді
3) Перетини в нижньому правому краї (12) - третє число відповіді.
Виходить: 2; 10; 12.
Оскільки два останніх числа - двозначні і ми не можемо їх записати, то записуємо тільки одиниці, а десятки додаємо до попереднього.
4. Італійський спосіб множення ( "Сіткою")
В Італії, а також у багатьох країнах Сходу, цей спосіб придбав велику популярність.
Наприклад, помножимо 6827 на 345.
1. Викреслює квадратну сітку і пишемо одне з чисел над колонками, а друга за висотою.
2. Множимо число кожного ряду послідовно на числа кожної колонки.
тобто- 6 * 3 = 18. Записуємо 1 і 8
- 8 * 3 = 24. Записуємо 2 і 4
Якщо при множенні виходить однозначне число, записуємо вгорі 0, а внизу це число.
(Як у нас в прикладі при множенні 2 на 3 вийшло 6. Вгорі ми записали 0, а внизу 6)
3. Заповнюємо всю сітку і складаємо числа, слідуючи діагональним смугах. Починаємо складати справа наліво. Якщо сума однієї діагоналі містить десятки, то додаємо їх до одиниць наступної діагоналі.
Цей прийом множення використовувався російськими селянами приблизно 2-4 століття назад, а розроблений був ще в глибоку давнину. Суть цього способу та: "На скільки ми ділимо перший множник, на стільки множимо другий" Ось приклад: Нам потрібно 32 помножити на 13. Ось як би вирішили цей приклад 3-4 століття тому наші предки:- 32 * 13 (32 ділимо на 2, а 13 множимо на 2)
- 16 * 26 (16 ділимо на 2, а 26 множимо на 2)
- 8 * 52 (і т.д.)
- 4 * 104
- 2 * 208
- 1 * 416 = 416
Розподіл навпіл продовжують до тих пір, поки в приватному не вийде 1, паралельно подвоюючи інше число. Останнє подвійну кількість і дає шуканий результат. Неважко зрозуміти, на чому цей спосіб заснований: твір не змінюється, якщо один множник зменшити вдвічі, а інший вдвічі ж збільшити. Ясно тому, що в результаті багаторазового повторення цієї операції виходить шукане твір
Однак що робити, якщо при цьому доводиться ділити навпіл число непарне? Народний спосіб легко виходить з цього утруднення. Треба, - говорить правило, - в разі непарного числа відкинути одиницю і ділити залишок навпіл; але зате до останнього числа правого стовпчика потрібно буде додати всі ті числа цього стовпця, які стоять проти непарних чисел лівого стовпця: сума і буде шуканим твором. Практично це роблять так, що всі рядки з парними лівими числами закреслюють; залишаються тільки ті, які містять наліво непарне число. Наведемо приклад (зірочки вказують, що даний рядок треба закреслити):- 19 * 17
- 9 * 34
- 4 * 68 *
- 2 * 136 *
- 1 * 272
- 17 + 34 + 272 = 323.
Такий спосіб множення використовували в Стародавній Індії.
Для множення, наприклад, 793 на 92 напишемо одне число як множимое і під ним інше як множник. Щоб легше орієнтуватися, можна використовувати сітку (А) як зразок.
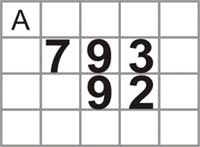
- Правило 1. Одиниці першого твору слід писати в тій же колонці, що і множник, тобто в даному випадку під 9.
- Правило 2. Подальше твори треба писати таким чином, щоб одиниці поміщалися в колонці безпосередньо праворуч від попереднього твору.
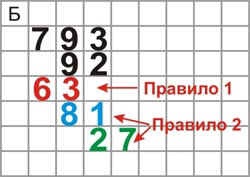
Повторимо весь процес з іншими цифрами множника, слідуючи тим же правилам (С).
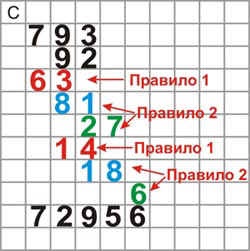
Потім складаємо цифри в колонках і отримуємо відповідь: 72956.
Як можна бачити, ми отримуємо великий список творів. Індійці, що мали велику практику, писали кожну цифру не в відповідну колонку, а зверху, наскільки це було можливо. Потім вони складали цифри в колонках і отримували результат.
Ми вступили в нове тисячоліття! Грандіозні відкриття і досягнення людства. Ми багато знаємо, багато вміємо. Здається чимось надприродним, що за допомогою чисел і формул можна розрахувати політ космічного корабля, "економічну - ситуацію" в країні, погоду на "завтра", описати звучання нот в мелодії. Нам відомий вислів давньогрецького математика, філософа, який жив в 4 столітті д. Н.е. Піфагора - "Все є число!".
Згідно філософського погляду цього вченого і його послідовників, числа керують не тільки мірою і вагою, але також усіма явищами, що відбуваються в природі, і є сутністю гармонії, що царює в світі, душею космосу.
Описуючи старовинні способи обчислень і сучасні прийоми швидкого рахунку, я спробував показати, що як в минулому, так і в майбутньому, без математики, науки створеної розумом людини, не обійтися.
"Хто з дитячих років займається математикою, той розвиває увагу, тренує мозок, свою волю, виховує наполегливість і завзятість у досягненні мети". (А.Маркушевіч)