У центрі стратегії - рівень коваріації дохідності активів портфеля. Інвестор знижує ризик портфеля, утримуючи прибутковість за допомогою поєднання активів з низькою кореляцією.
Ефективний портфель Марковіца: портфель, при заданому рівні ризику має максимальну очікувану прибутковість. Модель будується на таких передумовах про поведінку інвестора:
- На рішення впливають тільки 2 параметри: ризик і прибутковість;
- Інвестор не схильний до ризику;
- Прагне до максимальної прибутковості при встановленому рівні ризику;
- Однакові погляди на очікувані прибутковості і ризик;
- У всіх єдиний інвестиційний горизонт.
Для ефективного портфеля з безлічі активів розраховується n (n-1) / 2 кількість варіацій.
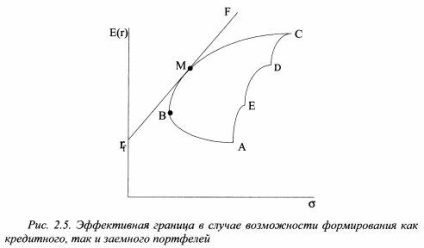
Якщо вкладник планує інвестувати кошти тільки в ризикований портфель, він повинен вибрати один з портфелів на ефективної кордоні ВС (див. Рис. 2.1), що відповідає його рівню ризику. У разі інвестування частини коштів в актив без ризику (актив Z з прибутковістю rf) на ефективної кордоні необхідно вибрати тільки один єдиний портфель, а саме, портфель М. Його можна знайти, провівши дотичну від значення ставки без ризику rf до ефективної кордоні Марківці. Інвестор вибере портфель М, так як кредитний портфель, складений з активу Z і портфеля M, дозволяє йому отримати вищу очікувану дохідність при тому ж рівні ризику, що і ризиковані портфелі, розташовані на відрізку ефективної кордону ВМ. Таким чином, при формуванні кредитного портфеля змінюється ефективна межа - з неї виключається відрізок ВМ, оскільки з'являються нові домінуючі портфелі. Ефективна межа представлена тепер лінією г / М. У свою чергу це означає, що в разі інвестування тільки в ризиковані активи, вкладник повинен вибирати портфелі тільки на ділянці МС.
Припустимо, вкладник не слід цього правила і формує портфель з активу без ризику (Z) і ризикованого портфеля, однак в якості ризикованого портфеля він вибирає не портфель М9 а портфель G (див. Рис. 2.2). Тоді всі можливі поєднання очікуваної прибутковості і ризику будуть розташовуватися на прямій r / G.
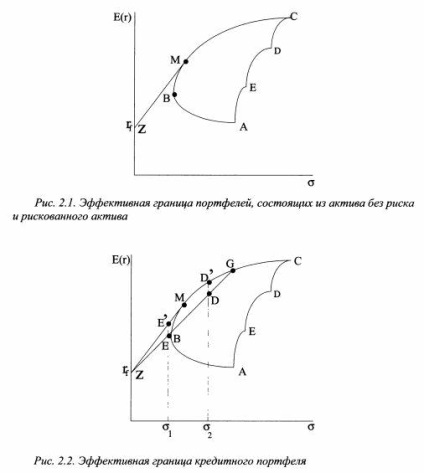
Як видно з рис. 2.2, дана стратегія не оптимальна, оскільки існують портфелі, розташовані на кордоні r / MG, домінуючі над портфелями на прямий rf G (за винятком точок / у і G). Так, якщо інвестор згоден на ризик А2, то портфель D 'буде домінувати над портфелем D. Тому вкладнику слід зупинити вибір тільки на ризикованому портфелі D \ а не на поєднанні активу без ризику і ризикованої портфеля G. Якщо він згоден на ризик <УХ. то портфель Е' будет доминировать над портфелем Е. Чтобы получить портфель Е\ следует комбинировать актив без риска с рискованным портфелем Л/, а не G.
Таким чином, якщо вкладник прагне сформувати кредитний портфель, то в якості ризикованого портфеля він повинен вибрати тільки портфель М.
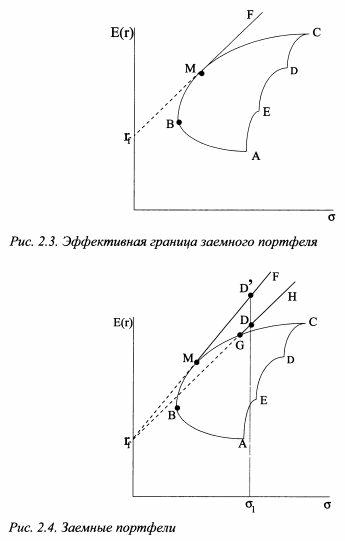
Припустимо тепер, що інвестор має можливість сформувати позиковий портфель. Він займає кошти під ставку / у і набуває ризикований портфель Л /. Тоді всі можливі портфелі розташовуються на прямій MF (див. Рис. 2.3), яка позначена суцільною лінією. Ризикований портфель М знаходимо, провівши дотичну з точки / у до ефективної кордоні. Припустимо, що інвестор формує позиковий портфель, придбаний не портфель Л /, а інший ризикований портфель на ефективної кордоні, наприклад портфель G (див. Рис. 2.4). Тоді він отримує доступ до будь-якого портфелю, розташованому на прямий GH, наприклад портфелю D. Однак дана стратегія не оптимальна, оскільки дня того ж рівня ризику (<т,) можно получить более высокую ожидаемую доходность, купив портфель D\. Но для этого следует инвестировать заемные средства только в портфель M.
Таким чином, якщо інвестор може сформувати як позиковий, так і кредитний портфелі, то з усіх ризикованих портфелів на ефективної кордоні він вибере тільки портфель М, а ефективна межа перетвориться в пряму лінію TfF (див. Рис. 2.5).