3. Плоска система довільно розташованих сил
Силу, прикладену до абсолютно твердого тіла, можна, не змінюючи чиниться дії, переносити паралельно їй самій в будь-яку точку тіла, додаючи при цьому пару з моментом, рівним моменту яку переносять сили щодо точки, куди сила переноситься (рис. 10).
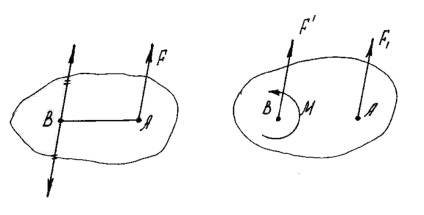
Будь-яка плоска система сил, що діють на абсолютно тверде тіло, при приведенні до довільно взятому центру Про замінює однією силою R. рівній головному вектору системи і прикладеною в центрі приведення О. і однією парою з моментом МО. рівним головному моменту системи відносно центру Про (рис. 11).
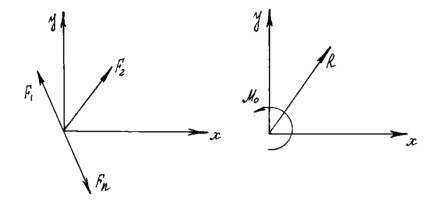
Окремі випадки приведення плоскої системи сил до найпростішого виду:
- якщо для даної системи сил R = 0 і МО = 0, то вона знаходиться в рівновазі;
- якщо для даної системи сил R ≠ 0, М = 0, то вона приводиться до однієї рівнодіючої.
Основна форма умов рівноваги. Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб сума проекцій всіх сил на кожну з двох координатних осей і сума їх моментів відносно будь-якого центру, лежачого в площині дії сил, дорівнювали нулю.
Друга форма умов рівноваги. Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб сума моментів всіх цих сил щодо якихось двох центрів А і В і сума їх проекцій на вісь Ох. НЕ перпендикулярну до прямої АВ. дорівнювали нулю.
Третя форма умов рівноваги. Для рівноваги довільної плоскої системи сил необхідно і достатньо, щоб сума моментів всіх цих сил щодо будь-яких трьох центрів А. В. С. не лежать на одній прямій, дорівнювали нулю.
4. Поняття про ферму. розрахунок ферм
Фермою називається жорстка конструкція з прямолінійних стрижнів, з'єднаних на кінцях шарнірами (рис. 12).
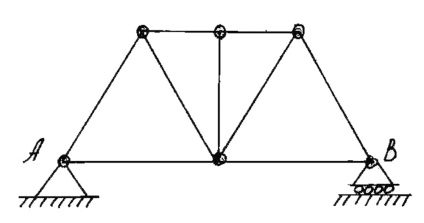
Якщо все стрижні ферми лежать в одній площині, ферма називається плоскою.
Місця з'єднання стрижнів ферми називають вузлами.
Похилі стержні називаються розкосами. вертикальні - стійками.
Відстань між двома опорами називається прольотом.
Розрахунок ферм виконується двома методами:
1) метод вирізання вузлів. який зводиться до послідовного розгляду умов рівноваги сил, що сходяться в кожному з вузлів ферми;
2) метод перетинів (метод Ріттера), який полягає в тому, що ферму поділяють на дві частини перетином, що проходить через три стрижня, в яких потрібно визначити зусилля, склавши рівняння рівноваги.
5. Просторова система сил
Моментом сили відносно осі називається скалярна величина, що дорівнює моменту проекції цієї сили на площину, перпендикулярну осі, взятому щодо точки перетину осі з площиною.
Щоб знайти момент сили відносно осі Z (рис. 13), треба:
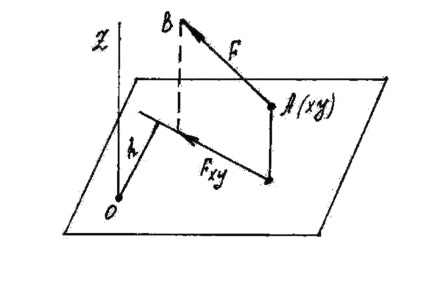
1) провести площину xy. перпендикулярну до осі z;
2) спроектувати силу F на цю площину і обчислити величину Fxy;
3) опустити з точки Про перетину осі з площиною перпендикуляр на напрям Fxy і його довжину h;
5) визначити знак моменту.
Окремі випадки при визначенні моменту:
1) якщо сила паралельна осі, то її момент відносно осі дорівнює нулю, так як Fxy = 0;
2) якщо лінія дії сили перетинає вісь, то її момент відносно осі також дорівнює нулю, так як h = 0;
3) якщо сила перпендикулярна до осі, то її момент відносно осі дорівнює добутку модуля сили на відстань між силою і віссю.
Умови рівноваги довільної просторової системи сил. Для рівноваги довільної просторової системи сил необхідно і достатньо, щоб суми проекцій всіх сил на кожну з трьох координатних осей і суми їх моментів відносно цих осей дорівнювали нулю.
II. Кінематика і твердого тіла
1. Основні поняття кінематики
1.1. Способи завдання руху точки
Кінематикою називається розділ механіки, в якому вивчаються геометричні властивості руху тіл без урахування їх інертності (маси) і діючих на них сил.
Кінематично задати рух або закон руху тіла (точки) означає задати положення цього тіла (точки) щодо даної системи відліку в будь-який момент часу.
Системою відліку називається реальне або умовне тверде тіло, по відношенню до якого визначається положення інших рухомих тел.
Природний спосіб завдання руху. Безперервна лінія, яку описує рухома точка щодо даної системи відліку, називається траєкторією точки. Якщо траєкторією є пряма лінія, рух точки називається прямолінійним, а якщо крива - криволінійним.
Закон руху точки вздовж траєкторії виражається рівнянням S = f (t).
Щоб задати рух точки природним способом, треба знати:
1) траєкторію точки;
2) початок відліку на траєкторії із зазначенням позитивного і негативного напрямків відліку;
3) закон руху точки вздовж траєкторії у вигляді S = f (t).
Чисельна величина швидкості точки в даний момент часу дорівнює першої похідної від відстані точки по часу:
Чисельна величина прискорення точки в даний момент часу дорівнює першої похідної від швидкості:
Координатний спосіб завдання руху
Закон руху точки при координатному способі виражається рівняннями:
Проекції швидкості на осі координат дорівнюють першим похідним від відповідних координат точки за часом:
Проекції прискорення на осі координат дорівнюють першим похідним від проекцій швидкостей або другим похідним від відповідних координат точки за часом.
1.2. Дотичне і нормальне прискорення точки
Проекція прискорення точки на дотичну до її траєкторії називається дотичним або тангенціальним ускореніема τ.
Проекція прискорення на нормаль називається нормальним ускореніема τ.
Дотичне і нормальне прискорення (рис. 14) розглядають не як проекції, а як складові повного прискорення. т. е. як векторні величини, і повне прискорення дорівнюватиме
Дотична складова спрямована по дотичній, як і вектор швидкості V. а тому не може впливати на напрямок швидкості, але впливає на її величину.
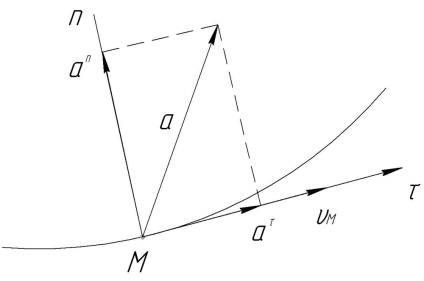
Нормальна складова спрямована перпендикулярно до вектора швидкості, а тому не може впливати на величину швидкості, але впливає на її напрямок.
, де ρ - радіус кривизни.
2. Поступальний і обертальний руху твердого тіла
Поступальним називається такий рух твердого тіла, при якому будь-яка пряма, проведена в цьому тілі, переміщається, залишаючись паралельною самій собі.
При поступальному русі всі точки тіла описують однакові (при накладенні збігаються) траєкторії і мають в кожен момент часу однакові по модулю і напрямку швидкості і прискорення.
При поступальному русі загальну для всіх точок тіла швидкість V називають швидкістю поступального руху тіла. а прискорення a - прискоренням поступального руху.
Обертальним називається такий рух твердого тіла, при якому будь-які дві точки, що належать тілу (або незмінно з ним пов'язані), залишаються в усі час руху нерухомими.
Пряма, що проходить через дві нерухомі точки, називається віссю обертання.
Рівняння γ = f (t) висловлює закон обертального руху твердого тіла. де γ - кут повороту тіла.
Основними кінематичними характеристиками обертального руху твердого тіла є його кутова швидкість ω і кутове прискорення ε.
Кутова швидкість тіла в даний момент часу чисельно дорівнює першої похідної від кута повороту за часом:
Кутове прискорення тіла в даний момент часу чисельно дорівнює першої похідної від кутової швидкості або другій похідній від кута повороту тіла за часом:
Якщо модуль кутової швидкості з часом зростає, обертання тіла називається прискореним. а якщо убуває - уповільненим.
Якщо кутова швидкість тіла залишається в усі час руху постійної (ω = const), то обертання тіла називається рівномірним.
Якщо кутове прискорення тіла в усі час руху постійно (ε = const), то обертання називається равнопеременное.
Лінійна швидкість точки v обертового твердого тіла чисельно дорівнює добутку кутової швидкості тіла ω на відстань R від цієї точки до осі обертання.
Лінійна швидкість направлена по дотичній до описуваної точкою кола або перпендикулярно до площини, що проходить через вісь обертання.
Так як для всіх точок тіла кутова швидкість ω має в даний момент одне і те ж значення, то слід, що лінійні швидкості точок крутного тіла пропорційні їх відстаням від осі обертання (рис. 15).
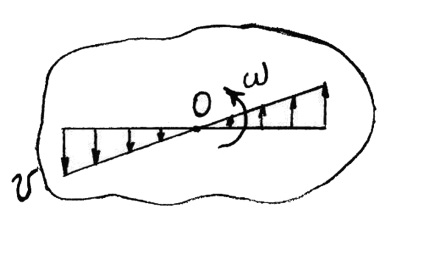
Дотичне ускореніеa τ направлено по дотичній до траєкторії (в сторону руху, якщо тіло обертається прискорено, або у зворотний бік, якщо тіло обертається уповільнено); нормальне прискорення an завжди направлено по радіусу R до осі обертання (рис. 16).
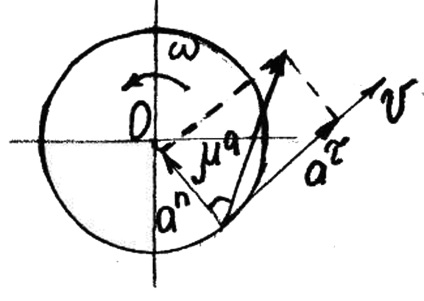
Повний прискорення точки дорівнює a = R.
Відхилення вектора повного прискорення від радіуса описуваної точкою кола визначається кутом μ, який обчислюється за формулою: