Площа трикутника дорівнює половині твори його сторін на синус кута між ними.
Розглянемо довільний трикутник ABC. Нехай в ньому сторона BC = a, сторона CA = b і S - площа цього трикутника. Необхідно довести, що S = (1/2) * a * b * sin (C).
Для початку введемо прямокутну систему координат і помістимо початок координат в точку С. Розташуємо нашу систему координат так, щоб точка B лежала на позитивному напрямку осі Сх, а точка А мала б позитивну ординату.
Якщо все виконати правильно, то повинен вийде наступний рисунок.
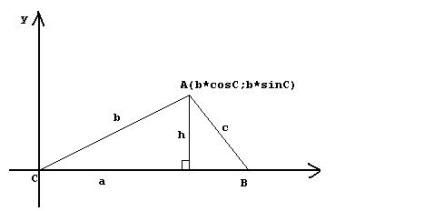
Площа даного трикутника можна обчислити за такою формулою: S = (1/2) * a * h. де h - це висота трикутника. У нашому випадку висота трикутника h дорівнює ординате точки А, тобто h = b * sin (C).
З огляду на отримані результат, формулу площі трикутника можна переписати таким чином: S = (1/2) * a * b * sin (C). Що й потрібно було довести.
Вирішення задач
Завдання 1. Знайти площу трикутника ABC, якщо а) AB = 6 * √8 см, АС = 4 см, кут А = 60 градусів б) BC = 3 см, AB = 18 * √2 см, кут B = 45 градусів в ) AC = 14 см, CB = 7 см, кут C = 48 градусів.
За доведеною вище теоремі площа S трикутника ABC дорівнює:
а) S = ((1/2) * 6 * √8 * 4 * sin (60˚)) = 12 * √6 см ^ 2.
б) S = (1/2) * BC * BA * sin (B) = ((1/2) * 3 * 18 * √2 * (√2 / 2)) = 27 см ^ 2.
в) S = (1/2) * CA * CB * sin (C) = ½ * 14 * 7 * sin48˚ см ^ 2.
Значення синуса кута вважаємо на калькуляторі або використовуємо значення з таблиці значень тригонометричних кутів. відповідь:
в) приблизно 36.41 см ^ 2.
Завдання 2. Площа трикутника ABC дорівнює 60 см ^ 2. Знайдіть сторону AB, якщо AC = 15 см, кут А = 30˚.
Покладемо S - площа трикутника ABC. По теоремі про площі трикутника маємо:
Підставами в неї наявні у нас значення:
60 = (1/2) * AB * 15 * sin30˚ = (1/2) * 15 * (1/2) * AB = (15/4) * AB.
Звідси висловлюємо довжину сторони AB: AB = (60 * 4) / 15 = 16.