Такий дивний і знайомий квадрат. Він симетричний щодо свого центру і осей, проведених по діагоналях і через центри сторін. А шукати площа квадрата або його обсяг взагалі не складає великих труднощів. Особливо якщо відома довжина його боку.
Кілька слів про фігуру і її властивості
Перші дві властивості пов'язані з визначенням. Всі сторони фігури рівні один одному. Адже квадрат - це правильний чотирикутник. Причому у нього обов'язково всі сторони рівні і кути мають однакове значення, а саме - 90 градусів. Це друга властивість.
Третє пов'язано з довжиною діагоналей. Вони теж виявляються рівними один одному. Причому перетинаються під прямими кутами і в точках середини.
Формула, в якій використовується тільки довжина сторони
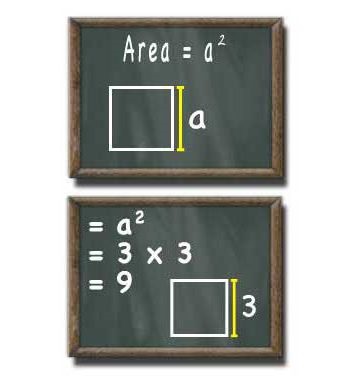
Спочатку про позначення. Для довжини сторони прийнято вибирати букву «а». Тоді площа квадрата обчислюється за формулою: S = а 2.
Вона легко виходить з тієї, що відома для прямокутника. У ній довжина і ширина перемножуються. У квадрата ці два елементи виявляються рівними. Тому у формулі з'являється квадрат цієї однієї величини.
Формула, в якій фігурує довжина діагоналі
Вона є гіпотенузою в трикутнику, катетами якого є сторони фігури. Тому можна скористатися формулою теореми Піфагора і вивести рівність, в якому сторона виражена через діагональ.
Провівши такі нескладні перетворення, отримуємо, що площа квадрата через діагональ обчислюється за такою формулою:
S = d 2 / 2. Тут буквою d позначена діагональ квадрата.
Формула по периметру
У такій ситуації необхідно висловити сторону через периметр і підставити його в формулу площі. Оскільки однакових сторін у фігури чотири, то периметр доведеться розділити на 4. Це буде значення боку, яку потім можна підставити в початкову і порахувати площу квадрата.
Формула в загальному вигляді виглядає так: S = (Р / 4) 2.
Завдання на розрахунки
№ 1. Є квадрат. Сума двох його сторін дорівнює 12 см. Обчисліть площу квадрата і його периметр.
Рішення. Оскільки дана сума двох сторін, то потрібно дізнатися довжину однієї. Так як вони однакові, то відоме число потрібно просто розділити на два. Тобто сторона даної фігури дорівнює 6 см.
Тоді його периметр і площу легко обчислюються за наведеними формулами. Перший дорівнює 24 см, а друга - 36 см 2.
Відповідь. Периметр квадрата дорівнює 24 см, а його площа - 36 см 2.
№ 2. Дізнайтеся площа квадрата з периметром, рівним 32 мм.
Рішення. Досить просто підставити значення периметра в написану вище формулу. Хоча можна спочатку дізнатися сторону квадрата, а вже потім його площа.
В обох випадках в діях спочатку буде йти розподіл, а потім зведення в ступінь. Прості розрахунки призводять до того, що площа представленого квадрата дорівнює 64 мм 2.
Відповідь. Шукана площа дорівнює 64 мм 2.
№ 3. Сторона квадрата дорівнює 4 дм. Розміри прямокутника: 2 і 6 дм. У який з цих двох фігур більше площа? На скільки?
Рішення. Нехай сторона квадрата буде позначена буквою а1. тоді довжина і ширина прямокутника А2 і В2. Для визначення площі квадрата значення а1 покладається звести в квадрат, а прямокутника - перемножити А2 і В2. Це не складно.
Виходить, що площа квадрата дорівнює 16 дм 2. а прямокутника - 12 дм 2. Очевидно, що перша фігура більше другий. Це при тому, що вони рівновеликі, тобто мають однаковий периметр. Для перевірки можна порахувати периметри. У квадрата сторону потрібно помножити на 4, вийде 16 дм. У прямокутника скласти боку і помножити на 2. Буде те саме число.
В задачі потрібно ще відповісти, на скільки площі розрізняються. Для цього з більшого числа віднімають менше. Різниця виявляється рівною 4 дм 2.
Відповідь. Площі рівні 16 дм 2 і 12 дм 2. У квадрата вона більше на 4 дм 2.
Завдання на доказ
Умова. На катеті рівнобедреного прямокутного трикутника побудований квадрат. До його гіпотенузі побудована висота, на якій побудований ще один квадрат. Довести, що площа першого в два рази більше, ніж другого.
Рішення. Введемо позначення. Нехай катет дорівнює а, а висота, проведена до гіпотенузи, х. Площа першого квадрата - S1. другого - S2.
Площа квадрата, побудованого на катеті, обчислюється просто. Вона виявляється рівною а 2. З другим значенням все не так просто.
Для початку потрібно дізнатися довжину гіпотенузи. Для цього знадобиться формула теореми Піфагора. Прості перетворення призводять до такого виразу: а√2.
Оскільки висота в трикутник, проведена до основи, є ще і медіаною і висотою, то вона ділить великий трикутник на два рівних рівнобедрених прямокутних трикутника. Тому висота дорівнює половині гіпотенузи. Тобто х = (а√2) / 2. Звідси легко дізнатися площа S2. Вона виходить рівною а 2/2.
Очевидно, що записані значення відрізняються рівно в два рази. Причому друга в це число раз менше. Що й потрібно було довести.
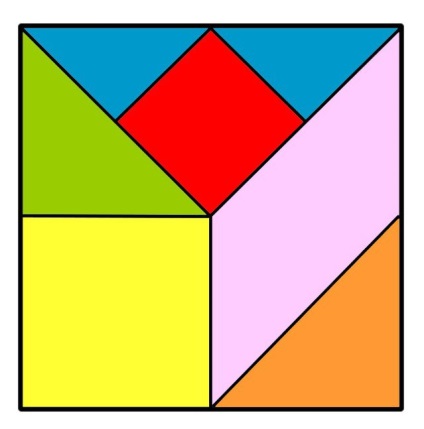
Незвичайна головоломка - танграм
Вона робиться з квадрата. Його необхідно за певними правилами розрізати на різні фігури. Всього частин повинно виявитися 7.
Правила передбачають, що в процесі гри будуть використовуватися всі отримані деталі. З них потрібно складати інші геометричні фігури. Наприклад, прямокутник, трапецію або паралелограм.
Але ще цікавіше, коли зі шматочків виходять силуети тварин або предметів. Причому виявляється, що площа всіх похідних фігур дорівнює тій, що була у початкового квадрата.
