Теорема Вієта. приклади розв'язання
У цій лекції ми познайомимося з цікавими співвідношеннями між країнами квадратного рівняння і його коефіцієнтами. Ці співвідношення вперше виявив французький математик Франсуа Вієт (1540-1603).

Наприклад, для рівняння Зx 2 - 8x - 6 = 0, не знаходячи його коренів, можна, скориставшись теоремою Вієта, відразу сказати, що сума коренів дорівнює. а твір коренів одно
т. е. - 2. А для рівняння х 2 - 6х + 8 = 0 укладаємо: сума коренів дорівнює 6, твір коренів одно 8; між іншим, тут неважко здогадатися, чому дорівнюють коріння: 4 і 2.
Доказ теореми Вієта. Коріння х1 і х2 квадратного рівняння ах 2 + b х + с = 0 знаходяться за формулами
де D = b 2 - 4ас - дискримінант рівняння. Склавши ці коріння,
отримаємо
Тепер обчислимо твір коренів х1 і х2 Маємо
Друге співвідношення доведено:
Зауваження. Теорема Вієта справедлива і в тому випадку, коли квадратне рівняння має один корінь (т. Е. Коли D = 0), просто в цьому випадку вважають, що рівняння має два однакових кореня, до яких і застосовують зазначені вище співвідношення.
Особливо простий вид приймають доведені співвідношення для наведеного квадратного рівняння х 2 + рх + q = 0. У цьому випадку отримуємо:
x1 = x2 = -p, x1 x2 = q
тобто сума коренів наведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, а твір коренів одно вільному члену.
За допомогою теореми Вієта можна отримати і інші співвідношення між країнами і коефіцієнтами квадратного рівняння. Нехай, наприклад, х1 і х2 - корені наведеного квадратного рівняння х 2 + рх + q = 0. Тоді
Однак основне призначення теореми Вієта не в тому, що вона виражає деякі співвідношення між країнами і коефіцієнтами квадратного рівняння. Набагато важливіше те, що за допомогою теореми Вієта виводиться формула розкладання квадратного тричлена на множники, без якої ми надалі не обійдемося.
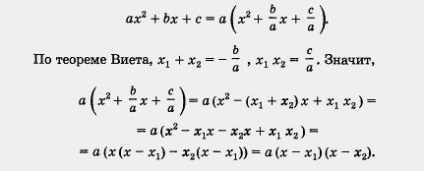
Приклад 1. Розкласти на множники квадратний тричлен Зх 2 - 10x + 3.
Рішення. Вирішивши рівняння Зх 2 - 10x + 3 = 0, знайдемо корені квадратного тричлена Зх 2 - 10x + 3: х1 = 3, х2 =.
Скориставшись теоремою 2, отримаємо
Є сенс замість написати Зx - 1. Тоді остаточно отримаємо Зх 2 - 10x + 3 = (х - 3) (3х - 1).
Зауважимо, що заданий квадратний тричлен можна розкласти на множники і без застосування теореми 2, використавши спосіб угруповання:
Зх 2 - 10x + 3 = Зх 2 - 9х - х + 3 =
= Зх (х - 3) - (х - 3) = (х - 3) (Зx - 1).
Але, як бачите, при цьому способі успіх залежить від того, чи зуміємо ми знайти вдалу угруповання чи ні, тоді як при першому способі успіх гарантований.
Приклад 1. Скоротити дріб
Рішення. З рівняння 2х 2 + 5х + 2 = 0 знаходимо х1 = - 2,
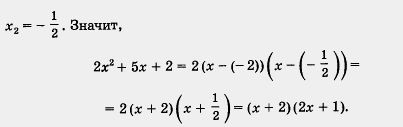
З рівняння х2 - 4х - 12 = 0 знаходимо х1 = 6, х2 = -2. Тому
х 2 - 4х - 12 = (х-6) (х - (- 2)) = (х - 6) (х + 2).
А тепер скоротимо задану дріб:
Приклад 3. Розкласти на множники вирази:
а) x4 + 5x 2 +6; б) 2x + -3
Р і ш е н і е. А) Введемо нову змінну у = х 2. Це дозволить переписати заданий вираз у вигляді квадратного тричлена щодо змінної у, а саме у вигляді у 2 + bу + 6.
Вирішивши рівняння у 2 + bу + 6 = 0, знайдемо корені квадратного тричлена у 2 + 5у + 6: у1 = - 2, у2 = -3. Тепер скористаємося теоремою 2; отримаємо
у 2 + 5у + 6 = (у + 2) (у + 3).
Залишилося згадати, що у = x 2. т. Е. Повернутися до заданого виразу. Отже,
x 4 + 5х 2 + 6 = (х 2 + 2) (х 2 + 3).
б) Введемо нову змінну у =. Це дозволить переписати заданий вираз у вигляді квадратного тричлена щодо змінної у, а саме у вигляді 2у 2 + у - 3. Вирішивши рівняння
2у 2 + у - 3 = 0, знайдемо корені квадратного тричлена 2у 2 + у - 3:
y1 = 1, y2 =. Далі, використовуючи теорему 2, отримаємо:
Залишилося згадати, що у =. т. е. повернутися до заданого виразу. Отже,
На закінчення параграфа - деякі міркування, знов-таки пов'язані з теоремою Вієта, а точніше, з зворотним твердженням:
якщо числа х1. х2 такі, що х 1 + х 2 = - р, x1 x2 = q, то ці числа - коріння рівняння
За допомогою цього твердження можна вирішувати багато квадратні рівняння усно, не користуючись громіздкими формулами коренів, а також складати квадратні рівняння з заданими корінням. Наведемо приклади.
2) х 2 + 11х + 30 = 0. Тут x1 + х2 = -11, х1 х2 = 30. Неважко здогадатися, що х1 = -5, х2 = -6.
Зверніть увагу: якщо вільний член рівняння - позитивне число, то обидва кореня або позитивні, або негативні; це важливо враховувати при підборі коренів.
3) х 2 + х - 12 = 0. Тут x1 + х2 = -1, х1 х2 = -12. Легко здогадатися, що х1 = 3, х2 = -4.
Зверніть увагу: якщо вільний член рівняння - негативне число, то коріння різні за знаком; це важливо враховувати при підборі коренів.
4) 5х 2 + 17x - 22 = 0. Неважко помітити, що х = 1 задовольняє рівняння, тобто х1 = 1 - корінь рівняння. Так як х1 х2 = -. а х1 = 1, то отримуємо, що х2 = -.
5) х 2 - 293x + 2830 = 0. Тут х1 + х2 = 293, х1 х2 = 2830. Якщо звернути увагу на те, що 2830 = 283 • 10, а 293 = 283 + 10, то стає ясно, що х1 = 283, х2 = 10 (а тепер уявіть, які обчислення довелося б виконати для вирішення цього квадратного рівняння за допомогою стандартних формул).
6) Складемо квадратне рівняння так, щоб його корінням служили числа х1 = 8, х 2 = - 4. Зазвичай в таких випадках складають наведене квадратне рівняння х 2 + рх + q = 0.
Маємо х1 + х2 = -р, тому 8 - 4 = -р, т. Е. Р = -4. Далі, х1 х2 = q, тобто 8 «(- 4) = q, звідки отримуємо q = -32. Отже, р = -4, q = -32, значить, шукане квадратне рівняння має вигляд х 2 -4х-32 = 0.