Граф може існувати в різних формах, що мають однакове число вершин, ребер, а також таке ж з'єднання краю. Такі графи називаються ізоморфні графи. Зверніть увагу, що ми називаємо графіки в цьому розділі в основному з метою посилаючись на них і визнання їх один від одного.
ізоморфними графами
Два графа G 1 і G 2 називаються ізоморфними. якщо -
- Їх кількість компонентів (вершин і ребер) однакові.
- Їх підключення краю зберігається.
Примітка - Коротше кажучи, з двох ізоморфних графів, один є пристосованими версія іншого. Немічених графік також можна розглядати як ізоморфна графа.
Ступінь послідовності G 1 і G 2 є однаковими.
Якщо вершини 1, V 2 ,. V до> утворюють цикл довжини K в G 1, то вершини 1), F (V 2) ,. F (V к)> повинні утворювати цикл довжини K в G 2.
Всі перераховані вище умови є необхідними для графів G 1 і G 2 ізоморфними, але не достатньо. щоб довести. що графи ізоморфні.
(G 1 ≡ G 2) тоді і тільки тоді. коли (G 1 - ≡ G 2 -). де G 1 і G 2 представляють собою прості графи.
(G 1 ≡ G 2). якщо матриці суміжності G 1 і G 2 є однаковими.
(G 1 ≡ G 2) тоді і тільки тоді. коли відповідні підграфи G 1 і G 2 (отриманий видаленням деяких вершин в G 1 і їх образи в графі G 2) ізоморфні.
Які з наступних графів ізоморфні?
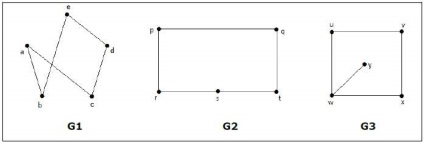
У графі G 3, вершини 'W' має тільки ступінь 3, тоді як всі інші вершин графа має ступінь 2. Отже. G 3. Не ізоморфна G 1 або G 2.
Беручи доповнення з G 1 і G 2, у вас є -
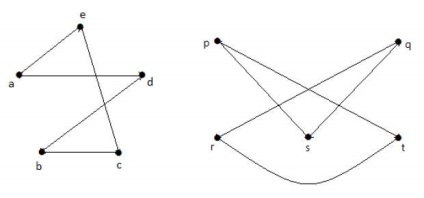
планарні графи
Граф 'G' називається планарним, якщо його можна намалювати на площині або сфери так, щоб ніякі два ребра не перетинаються один з одним в точці, що не вершинної.
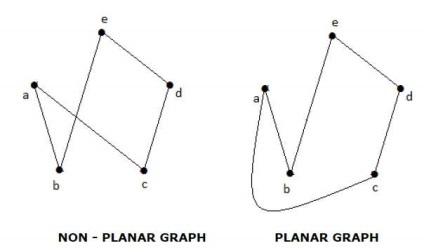
Кожен плоский граф розбиває площину на з'єднаних областей, званих регіонами.
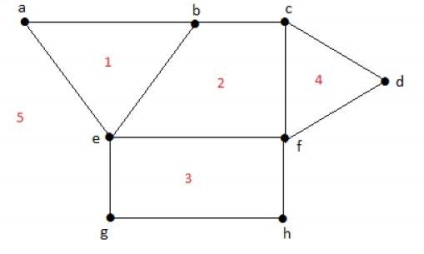
Ступінь обмеженою областіг = град (г) = Кількість ребер вміщають регіони р
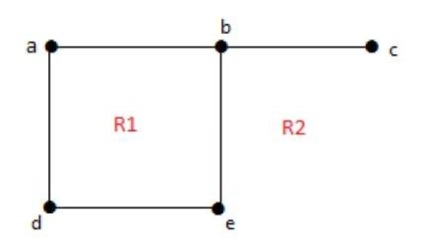
Ступінь необмеженої областіг = град (г) = Кількість ребер вміщають регіони р
У плоских графів, мають місце такі властивості добре -
1. У плоскому графі з 'N' вершин, сума ступенів усіх вершин
п Σ = 1 град (V г) = 2 | E |
2. Відповідно до сума ступенів регіонів теореми, в плоскому графі з 'п' областей, сума ступенів регіонів -
п Σ = 1 град (г г) = 2 | E |
Виходячи з наведеного вище теореми, можна зробити наступні висновки -
У плоскому графі,
Якщо ступінь кожної області К, то сума ступенів регіонів
Якщо ступінь кожної області, по крайней мере K (≥ K), то
Якщо ступінь кожної області становить не більше K (≤ K), то
Примітка - Припустимо. що всі регіони мають однаковий ступінь.
3. Відповідно до Формул Ейлера на плоских графів,
Якщо граф 'G' є зв'язковою плоскою, то
| V | + | R | = | E | + 2
Якщо плоский граф з компонентами 'K', то
| V | + | R | = | E | + (К + 1)
Де, | V | це число вершин, | E | це число ребер, і | R | це число регіонів.
4. Прикордонний Vertex нерівність
Якщо 'G' є зв'язковою плоский граф зі ступенем кожної області по крайней мере, 'K', то,
Ви знаєте, | V | і плюс; | R | = | E | і плюс; 2
K (| E | - | V | плюс; 2) ≤ 2 | E |
(K - 2) | E | ≤ K (| V | - 2)
5. Якщо 'G' є простою зв'язний плоский граф, то
Там існує, принаймні одна вершина V ∈ G, такий, що град (V) ≤ 5
6. Якщо 'G' є простою зв'язний плоский граф (по крайней мере 2 ребер) і без трикутників, то
7. Теорема Куратовского
Граф 'G' не є плоскою тоді і тільки тоді. коли 'G' має підграф, гомеоморфними K 5 або K 3,3.
гомоморфізм
Два графа G 1 і G 2 називаються гомоморфності, якщо кожен з цих графіків можуть бути отримані з того ж графа 'G', розділивши деякі ребра G з великою кількістю вершин. Погляньте на наступний приклад -
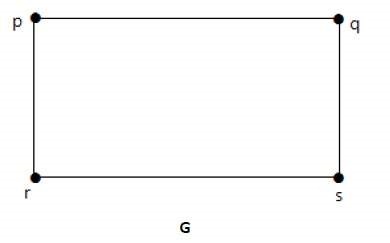
Розділіть край "RS" на два ребра, додавши одну вершину.
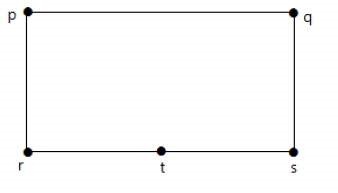
Графіки, показані нижче, гомоморфності першого графіка.
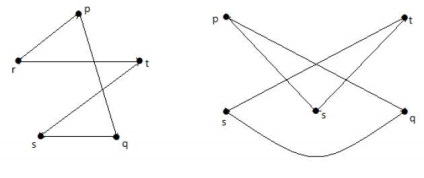
Якщо G 1 ізоморфна G 2, то G гомеоморфним G 2. але зворотне не обов'язково повинен бути правдою.
Будь-граф з 4-менш вершин є плоскою.
Будь-граф з 8 або менше ребер є плоскою.
Повний граф До п є плоскою тоді і тільки тоді. коли п ≤ 4.
Повний двочастковий граф K т, п є плоскою тоді і тільки тоді. коли т ≤ 2 або п ≤ 2.
Простий непланарная граф з мінімальним числом вершин є повний граф K 5.
Простий непланарная граф з мінімальним числом ребер K 3, 3.
багатогранні графік
Простий підключений плоский граф називається багатогранним графом, якщо ступінь кожної вершини ≥ 3, тобто, град (V) ≥ 3 ∀ V ∈ G.