Будь-яка система, що припускає наявність дискретних станів або наявність вузлів і переходів між ними може бути описана графом. З'єднання між вузлами (V) графа називаються ребрами (E). Якщо вузли графа не нумеровані, то ребра є неорієнтованими. У графа з нумерований вузлами ребра орієнтовані і називаються дугами
(Рис. 2).
Пара вершин може бути з'єднана двома або більше ребрами (дугами), такі ребра (дуги) називаються кратними. Вершини, з'єднані ребром (дугою) називаються суміжними. Якщо ребро починається і закінчується в одній і тій же вершині, то називається петлею.
Число ребер, що виходять з вершини vi (петля враховується двічі), називається валентністю (ступенем вершини) і позначається: d (vi).
Якщо V і E кінцеві безлічі, то і граф їм відповідний називається кінцевим. Граф називається виродженим. якщо він не має ребер.
Неорієнтовані граф називається простим. якщо він не має петель і будь-яка пара вершин з'єднана не більше ніж одним ребром. Графи відображаються на площині набором точок і з'єднують їх ліній або векторів. Грані можуть відображатися і кривими лініями, а їх довжина не має ніякого значення. Граф G називається планарним (плоским). якщо його можна відобразити в площині без перетину його граней (рис. 5). Граф називається зв'язковим. якщо для будь-яких двох вершин існує послідовність ребер їх з'єднує (рис. 3), тобто граф не має ізольованих фрагментів (вершин, ребер). Граф називається повним. якщо будь-які дві вершини з'єднані тільки одним ребром (рис.4). Якщо повний граф має n вершин, то кількість ребер дорівнюватиме n (n-1) / 2. Спеціальними видами графів є дерева (рис. 6), кільця і списки, що не входить в розгляд нашого курсу.
Граф, у якого все вершини мають одну і ту ж ступінь, називається регулярним графом.
Часто на одному безлічі об'єктів визначено кілька різних бінарних відносин. Для подання такої ситуації служать мультиграфом. Мультиграфом будуть використовуватися для подання діаграм кінцевих автоматів.
Ребро (дуга) і будь-яка з його вершин називаються інцидентними. Прийнято говорити, що (дуга) ребро (u. V) з'єднує вершини u і v. Якщо вершини не инцидентна жодному ребру (дузі), то вона називається ізольованою (d (vi) = 0), якщо належить тільки одному ребру (дузі), то називається висячої (d (vi) = 1).
Основні положення про вершинах графа:
1. У графі G сума ступенів усіх його вершин - число парне, рівне подвоєному числу ребер графа, так як кожне ребро бере участь в цій сумі рівно два рази. Цей результат називають леммой про рукостискання: якщо кілька людей потисли один одному руки, то загальне число потиск рук обов'язково парне, бо в кожному рукостисканні беруть участь дві руки (при цьому кожна рука вважається стільки раз, скільки вона брала участь в рукостискання).
2. Число непарних вершин будь-якого графа парне.
3. У всякому графі з n вершинами, де n ³2, завжди знайдуться, щонайменше, дві вершини з однаковими ступенями.
4. Якщо в графі з вершинами n> 2 дві вершини мають однаковий ступінь, то в цьому графі завжди знайдеться або одна вершина ступеня 0, або одна вершина ступеня n - 1.
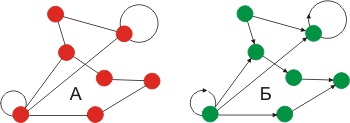
Два графа G1 = (V1, E1) і G2 = (V2, E2) називаються ізоморфними. якщо між їх вершинами існує взаємно однозначна відповідність.
Алгоритм розпізнавання ізоморфізму двох графів G1 (X, E) і G2 (Y, E)
1. Якщо X ≠ Y, то граф не ізоморфні.
2. Виписуємо всі елементи обох графів, визначаючи пари (xi, xj) і (yi. Yj) для кожного елемента, де xi. yi - число випадків для кожної вершини обох графів, а xj. yj - число заходів.
3. Для кожного елемента x графа G1 шукаємо такий елемент y графа G2. що виконується умова: число випадків x збігається з числом результатів y, і число заходів x збігається з числом заходів y. Знайдені елементи x та y з'єднуємо дугою, тобто будуємо граф відповідності. Якщо відповідності немає, то графи неізоморфних.
4. Виписуємо підстановку, яка переводить граф G1 в граф G2.
Приклади виконання завдань