[Ред] Опис
[Ред] Теорія
[Ред] сідловою
Сідлова точка матриці - це формально такий елемент матриці, що в своєму стовпці він найбільший (один з найбільших, тобто не строго>), а в своєму рядку він один з найменших. Наприклад в матриці
сідлова точка - це елемент в першому стовпці другому рядку, так як він> = усіх інших елементів першого стовпця і <= всех остальных элементов второй строки. Довольно просто показать, что если у матрицы несколько седловых точек, то все их значения равны. Для поиска всех седловых точек в матрицах большой размерности не нужно рассматривать каждый элемент отдельно, можно воспользоваться алгоритмом, опирающимся на вспомогательную теорему. Работу алгоритма покажем на примере поиска всех седловых точек матрицы
Зберемо найменші значення по всіх рядках, отримаємо (-4, 2, 2, -3). Також зберемо найбільші значення по всіх стовпцях (7, 2, 7, 2). Перевіримо, чи рівне найбільше з чисел першого набору найменшому числу з другого набору. У нашому випадку це так і це число 2. Якби виявилося, що максимум першого набору менше, ніж мінімум другого, то сідлових точок не було б. А ситуації, що максимум першого набору більше мінімуму другого взагалі бути не може, доводиться окремо. Отже, тепер подивимося, на яких позиціях стоять 2-ки в наших наборах. У першому це. а в другому це. На творі цих множин і розташовуються всі сідлові точки (тобто X = <. . .> )
Але до чого тут теорія ігор? Справа в тому що при грі один-на-один, коли інтереси гравців прямо протилежні ми користуємося матрицями стратегій і поняттям сідлових точок. Наприклад при грі в "камінь ножиці папір" матриця стратегій виглядає так
де стратегія - це безпосередньо вибір каменю, ножиць або паперу, а на перетинах стратегій виграш першого гравця. перший гравець вибирає рядок, другий вибирає стовпець. Можна перевірити, що у цій матриці немає сідлових точок. Як і майже у всіх матриць цікавих ігор один-на-один. Але уявімо, що матриця буде виглядати трохи по іншому
І на перетинах стратегій розмір виграшу першого гравця в рублях. Тобто, якщо перший гравець вибрав папір і другий гравець вибрав папір, то другий платить першому 2 рубля. А якщо перший гравець вибрав ножиці, а другий камінь, то перший гравець платить другому 1 рубль. Зрозуміло, що перший гравець відразу ж зрозуміє, що треба весь час показувати папір, так як тоді він буде тільки вигравати. А другий, намагаючись програти менше, буде показувати камінь, так як показавши камінь, він програє рубль, а не два. Як ви напевно вже здогадалися, точка в першому рядку другому стовпці - сідлова (можете перевірити). Гравці в гонитві за вигодою обиратимуть стратегії так, що на їх перетині будуть перебувати сідлові точки. А значення в цій точці (в даному випадку 1) називається значенням гри. Трійка називається рішенням гри. У нашому випадку це (або що теж саме).
Але ми досить сильно спотворили матрицю стратегій, а значить і правила, гри "камінь ножиці папір". Рідкісний людина захоче брати участь в ній в ролі Гравця 2. Наші корективи зробили гру несправедливою. Наявність сідлової точки, як правило, свідчить про несправедливість гри
[Ред] Змішані стратегії
Коли сідлових точок немає, починається пошук ймовірностей, з якими треба розподілити стратегії, щоб забезпечити найбільший виграш. Тобто вже зрозуміло, що немає "чарівної" стратегії, відповідної на всі випадки життя, і що треба вибирати різні стратегії з різними можливостями

[Ред] Методи рішення матричних ігор
Графічний алгоритм показаний на прикладі вирішення другого завдання з контрольної.
Також існує спосіб викидати неінформативні рядки і стовпці з матриці стратегій. Для цього нам потрібно поняття слабкого домінування і опуклою комбінації:
- Вектор a слабо домінує вектор b. якщо будь-який i-ий елемент а більше або дорівнює i-му елементу b.
- Опуклою комбінацією називають лінійну комбінацію векторів, в якій коефіцієнти невід'ємні і в сумі дають одиницю. Наприклад 0.2a + 0.3b + 0.5c це опукла комбінація векторів a. b і c
Отже, рядок ми можемо викинути, якщо існує опукла комбінація інших рядків, слабо домінуюча цей рядок. А стовпець ми можемо викинути, тільки якщо він слабо домінує якусь опуклу комбінацію інших стовпців.

[Ред] Завдання
[Ред] Завдання 1
[Ред] Пункт а
Відповісти на питання і обгрунтувати, чи може у матриці N xN бути рівно (округлено вгору) сідлових точок?
- Для парного N так, так як це рівно половина елементів матриці. Так що заповнимо ліву половину нулями, а праву одиницями. Отримаємо точно потрібну кількість елементів, так як всі нулі у нас - найбільші в шпальтах і найменші в рядках
- Для непарного N немає, так як метод знаходження сідлових точок, описаний в розділі Теорія, заснований на теоремі, наслідком з якої є те, що безліч сідлових точок представляється як прямокутник, тобто безліч точок [x, y] де x належить X. а y належить Y. тобто кількість сідлових точок має розкладатися на два множники, обидва з яких менше або дорівнюють N. Таким чином, у матриці 3x3 не може бути 7 сідлових точок, так як 7 - просте число. А для N = 25 = 313, а це число не ділиться без остачі ні на одне з чисел від 2 до 25
[Ред] Пункт б
Відповісти на питання і обгрунтувати, чи може у матриці N xN же не бути сідлових точок?
Так звичайно. І це навіть не залежить від N (при N> 1). приклад
Будь 0 є найменшим у своєму рядку, але не є найбільшим в своєму стовпці.
Будь-яка 1 є найбільшою в своєму стовпці, але не є найменшою в своєму рядку.
[Ред] Пункт в
Відповісти на питання і обгрунтувати, чи може у матриці N xN бути рівно одна сідлова точка?
Так звичайно. І це навіть не залежить від N. Приклад
Єдина сідлова точка тут це 1 (легко перевірити)
[Ред] Завдання 2
Знайти рішення гри для матриці стратегій
Будемо вирішувати для N = 25, але насправді тут мало що залежить від N. Ми бачимо, що тут немає сідлових точок, а значить рішення існує (причому обов'язково) тільки в змішаних стратегіях
Скористаємося графічним методом, який розрахований на матриці 2xn і m x2
Використовуючи коефіцієнти з трьох стовпців нашої матриці, запишемо три рівняння прямих
Обчисливши точки перетину, побудуємо графіки (p приймає значення від 0 до 1)
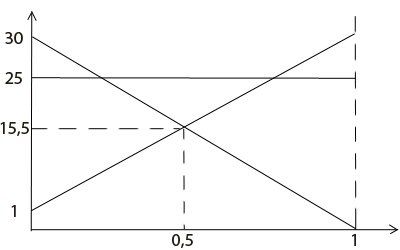
З усіх перетинів вибираємо ті, під якими не проходять інші прямі, і з них вибираємо те, що лівіше. У нашому випадку все просто, це перетин прямих l1 і l3. Значення p в цій точці 1/2, а значить розподіл стратегій першого гравця у нас P = p. 1-p> =. Значення гри у нас 15,5 (значення l1 або l3 в точці перетину). Залишилося знайти розподіл стратегій другого гравця. Для цього нам треба вирішити ще одне рівняння. У нас перетнулися прямі l1 і l2, тому візьмемо перший і третій стовпець початкової матриці. У кожному з них з верхнього елементу віднімемо нижній (так ми отримуємо коефіцієнти для рівняння другого гравця): k1 = 1 - 30 = -29, k3 = 30 - 1 = 29. Підставами їх в рівняння
тепер Q = q. 0, 1 -q> (для прямих, які не брали участі в перетині проставляем нульову ймовірність), отже Q =
P.S. Є рішення ще простіше. Якщо N> 15, то можна викинути середній стовпець, тому що він домінує полусумму першого і третього стовпчика. Тоді у нас виходить циклічна матриця 2x2, яка легко вирішується і без графічного методу