На попередніх заняттях ми вирішували тригонометричні нерівності наступних видів:
На цьому занятті ми будемо вирішувати нерівності виду tgt> a.
Будемо застосовувати наступний алгоритм вирішення (як на минулому уроці):
1. Якщо аргумент - складний (відмінний від х), то замінюємо його на t.
3. Знаходимо проміжок значень t. при яких тангенсоіда розташовується вище прямої у = а. Ліва межа цього проміжку arctg a. а права завжди (π / 2)
4. Записуємо подвійне нерівність для аргументу t. враховуючи найменший період тангенса Т = π (t буде між абсциссами arctg a і (π / 2)).
5. Робимо зворотну заміну (повертаємося до первісного аргументу) і висловлюємо значення х з подвійного нерівності, записуємо відповідь у вигляді числового проміжку.
Розділимо обидві частини нерівності на 3. Зробимо заміну даної змінної на t. Тоді отримаємо більш просте нерівність.
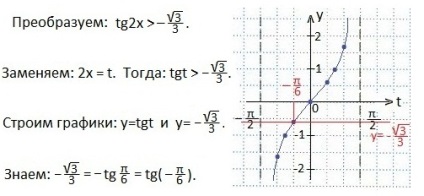
Визначимо проміжок значень змінної t. при яких нерівність буде вірним. Це абсциси тих точок графіка функції y = tg t. які лежать вище нашим прямим. Покажемо штрихуванням ці значення t. Запишемо знайдені значення аргументу t у вигляді подвійного нерівності.
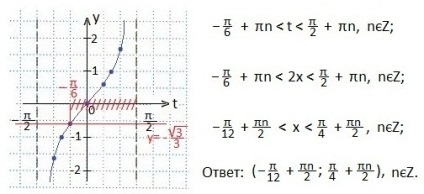
Перетворимо ліву частину нерівності за формулою tg (α + β) і отримаємо більш просте нерівність. Робимо заміну змінної.

Визначаємо шуканий проміжок значень змінної t. Потім висловимо х і запишемо відповідь у вигляді проміжку. Врахуємо, що нерівність Нечитка, але що тангенса (π / 2) не існує.

Застосовуємо правило для формул приведення:
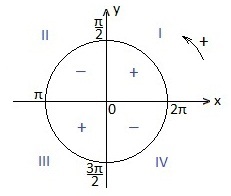
Наш аргумент знаходиться в 3-їй чверті, а котангенс в 3-їй чверті має знак «плюс». тому, знак наведеної функції не зміниться. У записі цього аргументу (π / 2) взято 3 рази (непарне число), тому функцію котангенс поміняємо на кофункцію - тангенс.
Тепер таку нерівність прийняло вид: tgt≥1. Побудуємо графіки функцій y = tgt і у = 1. Визначимо проміжок значень аргументу t. при яких нерівність tgt≥1 буде вірним. Відповідь запишемо у вигляді проміжку. Нерівність у нас Нечитка, але правий кінець проміжку не входить в рішення нерівності, так як тангенса (π / 2) не існує.
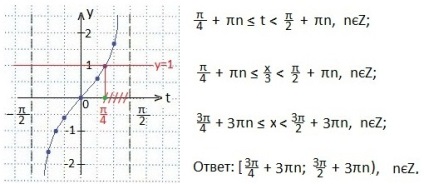
Любі друзі! Ми вирішили нерівності з тангенсом графічним способом, але, звичайно, існує і більш короткий рішення - за формулами.
якщо tgt Якщо tgt> a. то arctg a + πn Вивчіть ці формули, і ви будете вирішувати тригонометричні нерівності з тангенсом швидше! Сторінка 1 з 1 1Схожі статті