Рішення тригонометричних нерівностей з тангенсом, математика-повторення

3. Знаходимо проміжок значень t. при яких тангенсоіда розташовується нижче прямої у = а. Ліва межа цього проміжку завжди (-π / 2). а права arctg a

4. Записуємо подвійне нерівність для аргументу t. враховуючи період тангенса Т = π (t буде між абсциссами (-π / 2) і arctg a).

5. Робимо зворотну заміну (повертаємося до первісного аргументу) і висловлюємо значення х з подвійного нерівності, записуємо відповідь у вигляді числового проміжку.

Рішення тригонометричних нерівностей графічним способом надійно страхує нас від помилок тільки в тому випадку, якщо ми грамотно побудуємо графіки.

Побудуємо графіки функцій y = tgx і у = 1. Детально розглянемо побудову тангенсоіди. Приготуємо координатну площину хОу наступним чином:

одиничний інтервал дорівнює двом клітинам; так як значення π≈3,14. то π на горизонтальній осі Ох буде зображуватися шістьма клітинами; половина π (це π / 2) - трьома клітинами. Одна клітина - це π / 6; півтори клітини - це π / 4; дві клітини будуть відповідати аргументу π / 3.

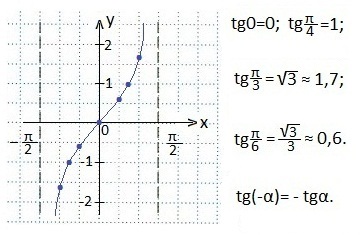
Ми знаємо, що тангенс 90 ° не існує, а так як функція тангенса періодична з найменшим періодом, рівним π. то не існує тангенс (90 ° + πn). Врахуємо це при побудові графіка і проведемо дві асимптоти. х = - π / 2 і х = π / 2.

Отже, в проміжку від - π / 2 до π / 2 тангенс буде «пробігати» всі свої значення. Користуючись значеннями тангенса деяких кутів і властивістю непарності функції тангенса (графік буде симетричний відносно початку координат), будуємо точки в приготовленої координатної площині, через які і проведемо тангенсоіду.

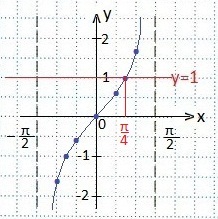
Проведемо її паралельно осі Ох. вище на один одиничний інтервал (вище на 2 клітини).

Пряма у = 1 перетинає тангенсоіду в точці з координатами (π / 4; 1).

Визначаємо проміжок значень х, при яких нерівність буде вірним, тобто всередині якого тангенсоіда розташовується нижче прямої у = 1. Врахуємо, що нерівність Нечитка, значить, правий кінець проміжку (π / 4) входить в безліч рішень нерівності. Записуємо рішення у вигляді подвійного нерівності. Відповідь запишемо у вигляді проміжку.

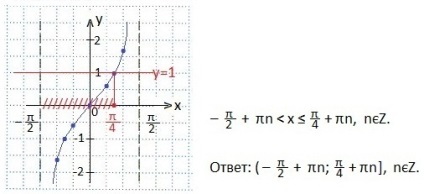
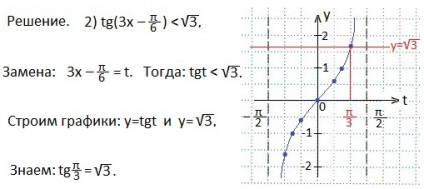
Відзначимо проміжок значень t. при яких точки тангенсоіди знаходяться нижче точок прямої у = 1. Запишемо цей проміжок у вигляді подвійного нерівності. Потім повторно його для початкового аргументу і висловимо х. Відповідь запишемо у вигляді проміжку.

Відзначаємо проміжок значень t. при яких нерівність вірно. У нас Нечитка нерівність, отже, правий кінець проміжку значень t також є рішенням нерівності. Повертаємося до первісного аргументу і висловлюємо х. Відповідь записуємо у вигляді проміжку значень змінної х.

Схожі статті