ТЕМА: «Види управління модельним часом.
Краснов С.П. ЗФ III курс 41гр.
Управління модельним часом
Види уявлення часу в моделі
Приступаючи до вивчення механізмів управління модельним часом, доречно поговорити про те, яку роль взагалі грає час в імітаційному моделюванні. При знайомстві з імітаційним експериментом ми відзначали, що він являє собою спостереження за поведінкою системи протягом певного проміжку часу. Звичайно, далеко не у всіх статистичних випробуваннях фактор часу t відіграє провідну роль, а в деяких і взагалі може не розглядатися. Згадайте, наприклад. задачу про обчислення площі кола: отриманий результат не залежав від того, як довго ми «бомбили» квадрат випадковими точками (мова в даному випадку не йде про кількість цих точок). Але значно більше завдань, в яких оцінка ефективності системи, що моделюється безпосередньо пов'язана з тимчасовими характеристиками її функціонування. До них відносяться згадувані вже завдання за оцінкою продуктивності, деякі завдання по оцінці надійності, якості розподілу ресурсів, а також всі завдання, пов'язані з дослідженням ефективності процесів обслуговування. Характерною особливістю більшості практичних завдань є те, що швидкість протікання розглянутих в них процесів значно нижче швидкості реалізації модельного експерименту. Наприклад, якщо моделюється робота обчислювального центру протягом тижня, навряд чи комусь прийде в голову відтворювати цей процес в моделі в такому ж масштабі часу. З іншого боку, навіть ті імітаційні експерименти, в яких тимчасові параметри роботи системи не враховуються, вимагають для своєї реалізації певних витрат часу роботи комп'ютера.
У зв'язку з цим при розробці практично будь-який імітаційної моделі і плануванні проведення модельних експериментів необхідно співвідносити між собою три вистави часу:
реальний час, в якому відбувається функціонування імітованої системи;
модельне (або, як його ще називають, системне) час, в масштабі якого організовується робота моделі;
машинний час, що відбиває витрати часу ЕОМ на проведення імітації.
За допомогою механізму модельного часу вирішуються наступні завдання:
відображається перехід модельованої системи з одного стану в інший;
виробляється синхронізація роботи компонент моделі;
змінюється масштаб часу «життя» (функціонування) досліджуваної системи;
здійснюється управління ходом модельного експерименту;
моделюється квазіпараллельний реалізація подій в моделі.
Приставка «квазі» в даному випадку відображає послідовний характер обробки подій (процесів) в ІМ, які в реальній системі виникають (протікають) одночасно.
Необхідність вирішення останнього завдання пов'язана з тим, що в розпорядженні дослідника знаходиться, як правило, однопроцесорна обчислювальна система, а модель може містити значно більше число одночасно працюючих підсистем. Тому дійсно паралельна (одночасна) реалізація всіх компонент моделі неможлива. Навіть якщо використовується так звана розподілена модель, реалізована на декількох вузлах обчислювальної мережі, зовсім не обов'язково, що число вузлів буде збігатися з числом одночасно працюючих компонент моделі. Трохи забігаючи вперед, слід зазначити, що реалізація квазіпараллельний роботи компонент моделі є досить складним технічним завданням. Деякі можливі методи її вирішення розглядаються в наступній лекції.
Існують два методи реалізації механізму модельного часу - з постійним кроком і з особливих станів.
Вибір методу реалізації механізму модельного часу залежить від призначення моделі, її складності, характеру досліджуваних процесів, необхідної точності результатів і т. Д.
Зміна часу з постійним кроком
При використанні даного методу відлік системного часу ведеться через фіксовані, вибрані дослідником інтервали часу. Події в моделі вважаються настали в момент закінчення цього інтервалу. Похибка у вимірюванні часових характеристик системи в цьому випадку залежить від величини кроку моделювання t.
Метод постійного кроку доцільно використовувати в тому випадку, якщо:
події з'являються регулярно, їх розподіл у часі досить одно- | мірно;
число подій велике і моменти їх появи близькі;
неможливо заздалегідь визначити моменти появи подій.
Даний метод управління модельним часом досить просто реалізувати в тому разі, коли умови появи подій всіх типів в моделі можна уявити як функцію часу.
Нехай, наприклад, подія полягає в тому, що летить літак перетинає деякий повітряний кордон, відстань до якого дорівнює R. Якщо літак рухається по прямій з постійною швидкістю V, можна обчислювати шлях, пройдений літаком, з інтервалом часу t: S = S + V -At. Відповідно, подія вважається наступившим, якщо виконується умова S> R, а момент часу настання події приймається рівним n-t, де n - номер кроку моделювання, на якому умова стало справжнім.
У загальному вигляді алгоритм моделювання з постійним кроком представлений на рис. 1 (- поточне значення модельного часу, - заданий інтервал моделювання), а для розглянутого вище прикладу з літаком - на рис. 2. Зверніть увагу на те, що на відміну від узагальненого алгоритму, в наведеному прикладі моделювання завершується не за фотографію в указаний час, а при настанні цікавить нас. У зв'язку з цим необхідно ще раз підкреслити, що при моделюванні з постійним кроком результат моделювання безпосередньо залежить від величини цього кроку. Причому, якщо крок буде занадто великим, то результат, швидше за все, буде невірним: момент закінчення чергового кроку дуже рідко буде збігатися з реальним моментом перетину літаком заданого кордону. Така ситуація показана на рис. 3.
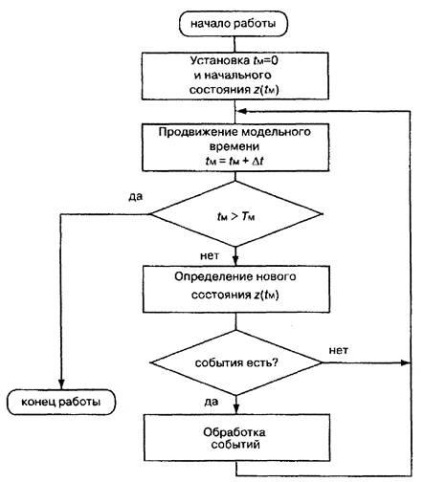
Мал. 1. Алгоритм моделювання з постійним кроком
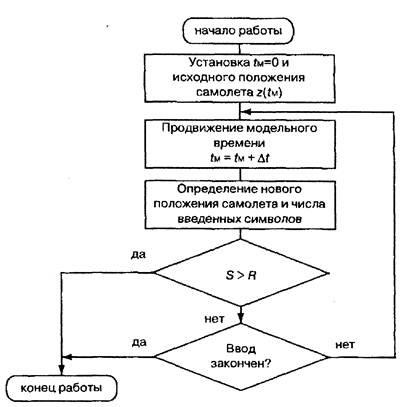
Мал. 2. Приклад моделювання з постійним кроком
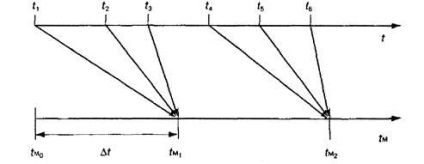
На малюнку використані наступні позначення:
tm1 -ось модельного часу при використанні кроку t1;
tm2 -ось модельного часу при використанні кроку t2
tp - вісь реального часу;
ТR - реальний момент перетину літаком кордону; ;
ТR1, TR2 - моменти перетину кордону, отримані для відповідних величин t.
Наведений приклад покликаний звернути увагу на те, що вибір величини кроку моделювання є нелегким і дуже важливою справою. Універсальної методики вирішення цієї проблеми не існує, але в багатьох випадках можна використовувати один з наступних підходів:
приймати величину кроку дорівнює середньому значенню інтенсивності виникнення подій різних типів;
вибирати величину кроку рівною середньому інтервалу між найбільш частим (або найбільш важливими) подіями.
Зміна часу з особливих станів
При моделюванні з особливих станів системне час кожен раз змінюється на величину, строго відповідну інтервалу часу до моменту настання чергового події. В цьому випадку події обробляються в порядку їх настання, а одночасно настали вважаються тільки ті, які є одночасними в дійсності.
Для реалізації моделювання з особливих станів потрібна розробка спеціальної процедури планування подій (так званого календаря подій). Якщо відомий закон розподілу інтервалів між подіями, то таке прогнозування труднощів не становить: досить до поточного значення модельного часу додати величину інтервалу, отриману за допомогою відповідного датчика.
Нехай, наприклад, за що летять літаком, фігурували при описі моделювання з постійним кроком, спостерігає диспетчер. Він вводить інформацію про літак, причому інтервали між введенням двох сусідніх повідомлень є випадковими величинами, розподіленими за нормальним законом з заданими параметрами Ілюстрація до такої ситуації наведена на рис. 4 (Тс - момент введення чергового повідомлення, t-випадковий інтервал).
Мал. 4. Зміна модельного часу з особливих станів.
Якщо ж момент настання події визначається деякими логічними умовами, то необхідно сформулювати ці умови і перевіряти їх істинність для кожного наступного кроку моделювання. Практика показує, що складності в реалізації механізму зміни часу з особливих станів пов'язані в першу чергу з коректним описом таких умов. Труднощі ще більш зростають, якщо в моделі фігурують кілька типів взаємопов'язаних подій.
Моделювання з особливих станів доцільно використовувати, якщо:
події розподіляються в часі нерівномірно або інтервали між ними великі;
пред'являються підвищені вимоги до точності визначення взаємного положення подій в часі;
необхідно враховувати наявність одночасних подій.
Додаткова перевага методу полягає в тому, що він дозволяє економити машинний час, особливо при моделюванні систем періодичної дії, в яких події тривалий час можуть не наступати.
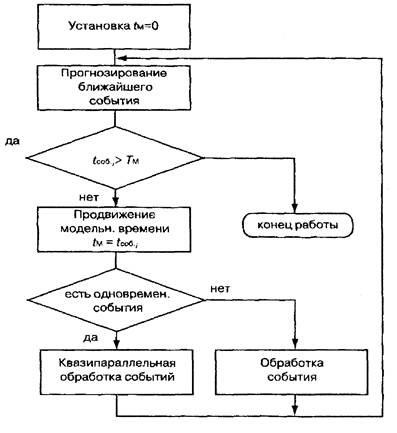
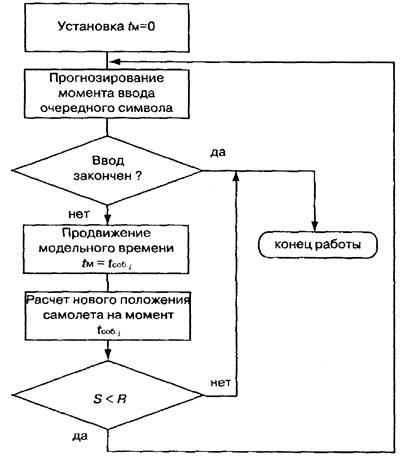
Узагальнена схема алгоритму моделювання з особливих станів представлена на рис. 5 (tco6.i - прогнозований момент настання i-го події).

Риc. 5. Алгоритм моделювання з особливих станів
Щоб «відчути різницю» в використанні двох методів управління модельним часом, повернемось до нашого прикладу з диспетчером. Доповнимо його наступною умовою: необхідно підрахувати число повідомлень, які встигне ввести диспетчер протягом заданого інтервалу моделювання.
Перш за все необхідно відповісти на питання: що розуміти під «особливими станами», які повинні впливати на зміну модельного часу? На практиці зазвичай замість станів розглядають події, що визначають зміну станів модельованого процесу. Для процесу введення інформації диспетчером такий перехід виконується досить просто: подія - це введення чергового повідомлення; іншими словами, введення чергового повідомлення «просуває» модельне час відповідний інтервал. Так, якщо інтервали між повідомленнями підкоряються нормальному закону з параметрами m і s, то чергове i-е значення модельного часу tm (i) визначається наступним чином:
У цьому виразі доданок norm (m, s) означає звернення до генератора чисел, розподілених за нормальним законом.
Алгоритм роботи моделі наведено на рис. 6 (N - число введених повідомлень).
Мал. 6. Приклад роботи моделі з особливих станів
Підіб'ємо підсумки викладеного в цьому розділі.
Вибір механізму зміни модельного часу визначає технологію реалізації імітаційної моделі.
На вибір методу моделювання впливає цілий ряд факторів, однак визначальним є тип модельованої системи: для дискретних систем, події в яких розподілені в часі нерівномірно, зручнішим є зміна модельного часу з особливих станів.
Якщо в моделі повинні бути представлені компоненти реальної системи, робота яких вимірюється в різних одиницях часу, то вони повинні бути попередньо приведені до єдиного масштабу.
Підсистема це фрагмент Simulink-моделі, оформлений у вигляді окремого блоку. Використання підсистем при складанні моделі має такі позитивні сторони:
Зменшує кількість одночасно відображаються блоків на екрані, що полегшує сприйняття моделі (в ідеалі модель повністю повинна відображатися на екрані монітора).
Дозволяє створювати і налагоджувати фрагменти моделі окремо, що підвищує технологічність створення моделі.
Дозволяє створювати власні бібліотеки.
Дає можливість синхронізації паралельно працюють підсистем.
Дозволяє включати в модель власні довідкові кошти.
Дає можливість пов'язувати підсистему з будь-яким m-файлом, забезпечуючи запуск цього файлу при відкритті підсистеми (нестандартне відкриття підсистеми).
Використання підсистем і механізму їх блоків дозволяє створювати блоки, які не поступаються стандартним за своїм оформленням (власне вікно параметрів блоку, піктограма, довідка тощо).
Кількість підсистем в моделі не обмежена, крім того підсистеми можуть включати в себе інші підсистеми. Рівень вкладеності підсистем один в одного також не обмежений.
Зв'язок підсистеми з моделлю (або підсистемою верхнього рівня ієрархії) виконується за допомогою вхідних (блок Inportбібліотекі Sources) і вихідних (блок Outport бібліотеки Sinks) портів. Додавання в підсистему вхідного або вихідного порту призводить до появи на зображенні підсистеми мітки порту, за допомогою якої зовнішні сигнали передаються всередину підсистеми або виводяться в основну модель. Перейменування блоків Inportілі Outportпозволяет змінити мітки портів, які відображаються на піктограмі підсистеми зі стандартних (In і Out) на ті, які потрібні користувачеві.
Підсистеми можуть бути віртуальними (Subsystem) і монолітними (AtomicSubsystem). Відмінність цих видів підсистем полягає в порядку виконання блоків під час розрахунку. Якщо підсистема є віртуальною, то Simulink ігнорує наявність кордонів відокремлюють таку підсистему від моделі при визначенні порядку розрахунку блоків. Іншими словами в віртуальній системі спочатку можуть бути розраховані вихідні сигнали декількох блоків, потім виконаний розрахунок блоків в основний моделі, а потім знову виконаний розрахунок блоків входять в підсистему. Монолітна підсистема вважається єдиним (неподільним) блоком і Simulink виконує розрахунок всіх блоків в такій підсистемі, не перемикаючись на розрахунки інших блоків в основний моделі. Зображення монолітної підсистеми має більш товсту рамку в порівнянні з віртуальної підсистемою.
Підсистеми можуть бути також керованими або некерованими. Керовані підсистеми завжди є монолітними. Керовані підсистеми мають додаткові (керуючі) входи, на які надходять сигнали активізують дану підсистему. Керуючі входи розташовані зверху або знизу підсистеми. Коли керована підсистема активізована - вона виконує обчислення. У тому випадку якщо керована підсистема пасивна, то вона не виконує обчислення, а значення сигналів на її виходах визначаються настройками вихідних портів.
Для створення в моделі підсистеми можна скористатися двома способами:
Скопіювати потрібну підсистему з бібліотеки Subsystem в модель.
Виділити за допомогою миші потрібний фрагмент моделі і виконати команду Create Subsystemіз менюEditокна моделі. Виділений фрагмент буде поміщений в підсистему, а входи і виходи підсистеми будуть забезпечені відповідними портами. Даний спосіб дозволяє створити віртуальну некеровану підсистему. Надалі, якщо це необхідно, можна зробити підсистему монолітної, змінивши її параметри, або керованої, додавши керуючий елемент з потрібною підсистеми знаходиться в бібліотеці. Скасувати угруповання блоків в підсистему можна командою Undo.
Мал. 7 ілюструє процес створення підсистеми другим способом. На рис. 8 показаний результат цього процесу. У прикладі використана модель керованого функціонального генератора.
Мал. 7 Створення підсистеми
Мал. 8 Модель, яка використовує підсистему