Короткий опис документа:
ТЕКСТОВА Розшифровка УРОКУ:
Сьогодні на уроці ми виведемо формулу для обчислення об'єму тіла за допомогою певного інтеграла і застосування формули до розв'язання задачі.
Згадаймо, що називається певним інтегралом.
Якщо функція f (x) неперервна на проміжку I числової осі, що містить точки х = а і х = b, то різниця значень F (b) -F (a) (де F (x) - первісна f (x) на I) називається певним інтегралом від функції f (x) від a до b.
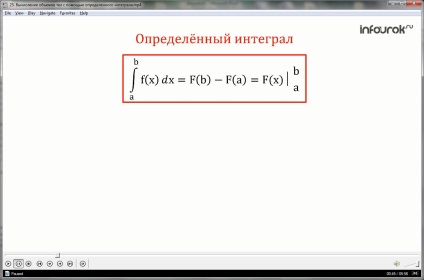
Це формула отримала назву Ньютона-Лейбніца.
(Інтеграл від a до b еф від ікс де ікс дорівнює різниці значень первісної еф велике від бе і а)
Виведемо основну формулу для обчислення обсягів тіл, засновану на понятті інтеграла: обсяг тіла дорівнює інтегралу від а до b площі підстави фігури де ікс,
Будемо розглядати довільне тіло об'ємом V, укладену між двома паралельними площинами яка перпендикулярна даними площинах.
а й b - абсциси точок перетину осі ох з цими площинами відповідно (а
Розглянемо перетин даного тіла площиною, перпендикулярній осі. в даному випадку Ф (х), цю фігуру ми будемо вважати або колом, або багатокутником. Позначимо площу цієї фігури S (x) = S (). Далі нам необхідно розділити відрізок [а; b] на n частин. Введемо позначення: а - це. b - це. Відстань між кожним дорівнюватиме
дельта х ітое дорівнює відношенню різниці а й b до n.

Далі розглянемо тіло, яке виходить між двома такими площинами. Відрізки розіб'ють тіло на n тел.
Розглянемо тіло, яке виходить між двома такими площинами T. Обсяг цього тіла наближено дорівнює обсягу призми, тобто площа підстави фігури, помножена на висоту дельта х ітое (довжину цього відрізка)
Тоді обсяг усього тіла наближено дорівнює сумі таких тел Т, тобто сумі по i від одного до n обсягів цих тіл, тобто сумі ес по х ітое на дельта х ітое, при цьому ми припускаємо, що ес від х ітое це безперервна функція на відрізку [а; b]
Межа цієї суми буде дорівнює обсягу цього тіла, але оскільки це межа інтегральної суми, то він дорівнює інтегралу від а до b ес від х Де х.

Таким чином, ми отримали формулу для обчислення обсягу довільного тіла через площу перпендикулярного перетину. Обсяг тіла дорівнює інтегралу від а до b площі підстави фігури Де х
Знайдемо обсяги тіл, використовуючи отриману формулу.
Знайти об'єм тіла, зображеного на малюнку, якщо перетин цього тіла площиною, перпендикулярної до осі Ох і проходить через точку з абсцисою х, є квадратом, сторона якого дорівнює.
Дано: перетин - квадрат
Рішення: розглянемо малюнок
На підставі виведеної нами формули обсяг тіла дорівнює певному інтегралу від а до b ес від х Де х
Площа квадрата будемо шукати за формулою
S (х) =. значить ес від х дорівнює квадрату сторони квадрата, підставимо замість а одиницю поділену на х. отримаємо
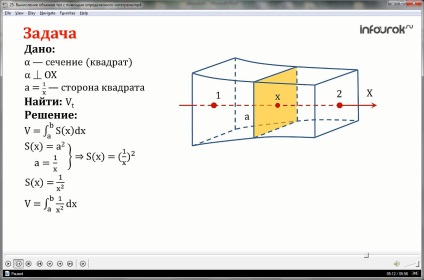
Підставами дане значення в формулу для знаходження об'єму за допомогою певного інтеграла: обсяг тіла дорівнює певному інтегралу від а до b від b у восьмому ступені Де х
Первісну статечної функції
Тоді формула (1), набуде вигляду: обсяг тіла дорівнює інтегралу від 1 до 2 одиниці поділеній на х в квадраті Де х, дорівнює мінус одиниці поділеній на х від 1 до 2, підставимо значення меж інтегрування два і один, отримаємо 0,5.