Матеріал з Вікіпедії - вільної енциклопедії

Лист Мебіуса (стрічка Мебіуса, петля Мьобіуса) -топологіческійоб'ект, простейшаянеоріентіруемаяповерхностьс краєм, одностороння при вкладенні в звичайне трёхмерноеевклідово пространствоR³. Потрапити з однойточкіетой поверхні в будь-яку іншу можна, не перетинаючи краю.
2Геометрія і топологія
5Іскусство і технологія
6Лента Мебіуса і знак нескінченності
Якщо розрізати стрічку вздовж по лінії, рівновіддаленої від країв, замість двох стрічок Мебіуса вийде одна довга двостороння (удвічі більше закручена, ніж стрічка Мебіуса) стрічка, яку називають «афганська стрічка». Якщо тепер цю стрічку розрізати вздовж посередині, виходять дві стрічки, намотание один на одного.
Якщо розрізати стрічку Мебіуса, відступаючи від краю приблизно на третину її ширини, то виходять дві стрічки, одна - більш тонка стрічка Мебіуса, інша - довга стрічка з двома півобертами (Афганська стрічка).
Інші цікаві комбінації стрічок можуть бути отримані зі стрічок з двома або більше півобертами в них. Наприклад якщо розрізати стрічку з трьома півобертами, то вийде стрічка, завита вузел трилисника. Розріз стрічки з додатковими оборотами дає несподівані фігури, названниепарадромнимі кільцями.
Геометрія і топологія
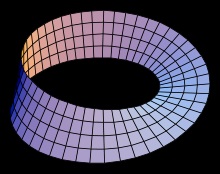
Параметричний опис листа Мебіуса.
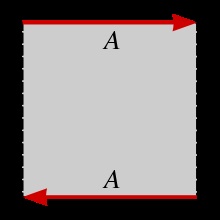
Щоб перетворити квадрат в лист Мебіуса, з'єднайте краї, помічені так, щоб напрямки стрілок збіглися.
Одним із способів подання листа Мебіуса як підмножини є параметризація:
де і. Ці формули задають стрічку Мебіуса ширини 1, чий центральний круг має радіус 1, лежить в плоскостіx-Yс центром в. Параметрuпробегает уздовж стрічки, в той час какvзадает відстань від краю.
Вціліндріческіх координатах, необмежена версія листа Мебіуса може бути представлена рівнянням:
Топологіческіліст Мебіус може бути визначений какфакторпространствоквадратапоотношенію еквівалентностідля.
Лист Мебіуса -неоріентіруемаяповерхностьс краєм.
Лист Мебіуса - це також простір нетрівіальногорасслоеніянад окружністю з шаром відрізок.
подібні об'єкти
Близьким «дивним» геометричним об'єктом являетсябутилка Клейна. Пляшка Клейна може бути отримана шляхом склеювання двох стрічок Мебіуса по краях. У звичайному трёхмерномевклідовом пространствесделать це, не створюючи самопересеченія, неможливо.
Інша схоже безліч -сфера з плівкою. Якщо проколоти отвір в сфері з плівкою, тоді те, що залишиться, буде листом Мебіуса. З іншого боку, якщо приклеїти диск до стрічки Мебіуса, поєднуючи їх межі, то результатом буде сфера з плівкою. Щоб візуалізувати це, корисно деформувати стрічку Мебіуса так, щоб її кордон став звичайним колом. Таку фігуру називають «пересічена кришка» (пересічена кришка може також означати ту саму фігуру з приклеєними диском, тобто погруженіепроектівной площині).
Існує поширена помилка, що пересічна кришка не може бути сформована в трьох вимірах без самопересекающиеся поверхні. Насправді можливо помістити стрічку Мебіуса в с кордоном, що є ідеальним колом. Ідея полягає в наступному: пустьCбудетедінічним кругомв плоскостіxyв. Соедінівантіподниеточкі наc, тобто, точки під угламіθіθ + πдугой кола, отримаємо, що дляθмежду0іπ / 2дугі лежать вище плоскостіxy, а для другіхθніже (причому в двох місцях дуги лежать в плоскостіxy).
Можна помітити, що якщо диск приклеюється до граничної кола, то самоперетинів получающейся сфери з плівкою неминуче в тривимірному просторі. У термінах завдання сторін квадрата, як було показано вище, сфера з плёнкойполучается склеюванням двох, що залишилися сторін ссохраненіеморіентаціі.