а) ((A B) (C A)) (B C);
б) ((((A B) A) B) C) C;
в) (A (B C)) ((A C) (A B)).
2. Привести до СДНФ і СКНФ формули:
3. За даним набору значень змінних побудувати елементарну кон'юнкцію, справжню тільки для цього набору значень змінних.
4. За даним набору значень змінних побудувати елементарну диз'юнкцію, неправдиву тільки для цього набору значень змінних.
5. Побудувати СКНФ і СДНФ, еквівалентні даній формулі, і знайти інтерпретації, на яких формула істинна і помилкова:
6. Для функцій g і h, визначених у таблиці 1, знайти СКН - і СДН - форми і найпростіші формули, що реалізують ці функції.
7. Скласти дві булеві функції, які планують 1-розрядний двійковий суматор по наступній таблиці
де x1 і x2 - однойменні розряди 1-го і 2-го доданків; e1 - одиниця переносу з молодшого розряду; e2 - одиниця перенесення в старший розряд суми; - результат підсумовування.
8. Побудувати формулу від трьох змінних, яка істинна в тому і тільки в тому випадку, коли рівно дві змінні помилкові.
9. Побудувати формулу від трьох змінних, яка приймає таке ж значення, як і більшість (меншість) змінних.
10. За СКНФ формули U побудувати:
а) СДНФ двоїстої формули U *;
б) СКНФ формули U;
в) СДНФ формули U.
11. За СДНФ формули U і СДНФ формули B побудувати:
а) СКНФ і СДНФ формули (U B);
б) СКНФ і СДНФ формули (U B);
в) СКНФ і СДНФ формули (U B).
3. Повні системи операцій
Система операцій називається повною. якщо будь-яка логічна операція може бути представлена формулою над .
Так як будь-яка формула може бути представлена наведеної формулою, то система 0 => - повна.
Система зводиться до *. позначається *. якщо всі операції системи * представимо формулами над системою . Якщо * повна, то і повна.
Останнє твердження дає один із способів докази повноти системи операцій - зведення її до відомої повній системі, наприклад до 0. Тобто повної буде система , через операції якої можна висловити кон'юнкцію, диз'юнкцію і заперечення.
Завдання. Довести повноту системи 5 =.
Рішення. Зведемо систему 5 до повної системі 0.
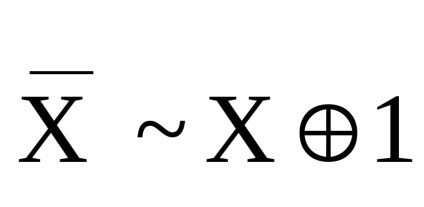
.
Якщо в довільній формулою алгебри Жегалкина, що реалізує булеву функцію f, розкрити дужки і зробити всі можливі спрощення, то вийде формула, що має вигляд суми творів, тобто полінома по mod 2. Така формула називається поліномом Жегалкина для даної функції. Лінійної називається функція, поліном Жегалкина якої лине.
Завдання. Уявити формулу (x1 x2) (
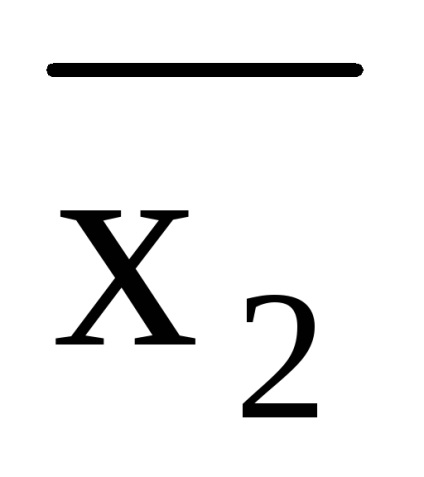
(X1 x2) (
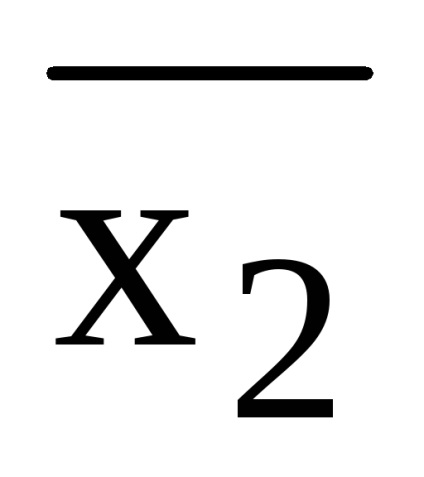
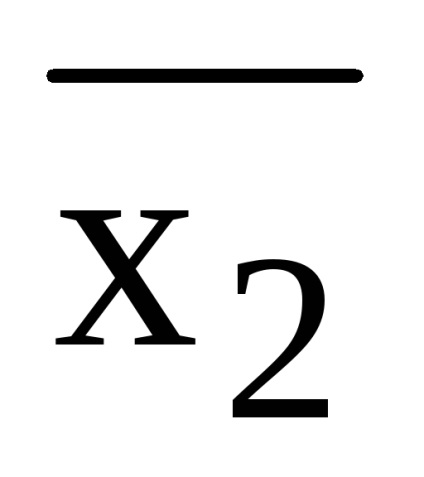
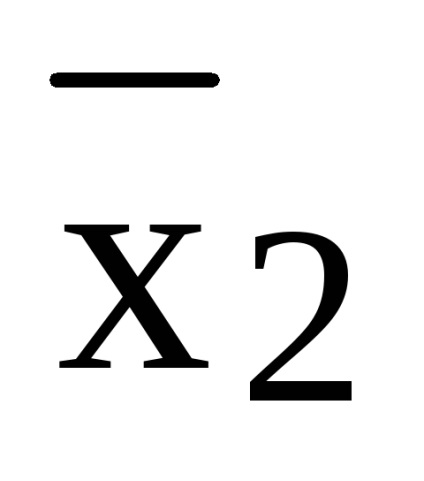
= X1 x2 x3 x1
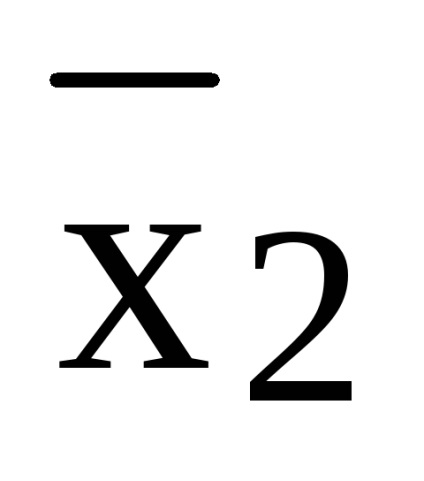
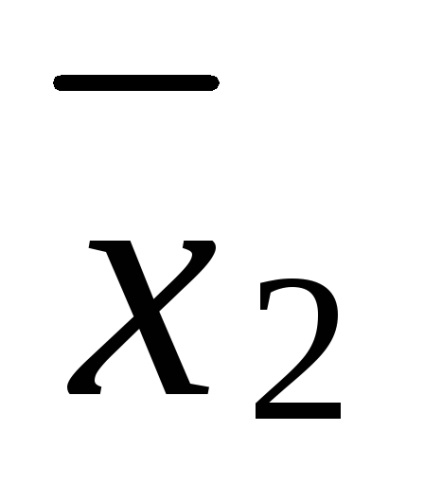
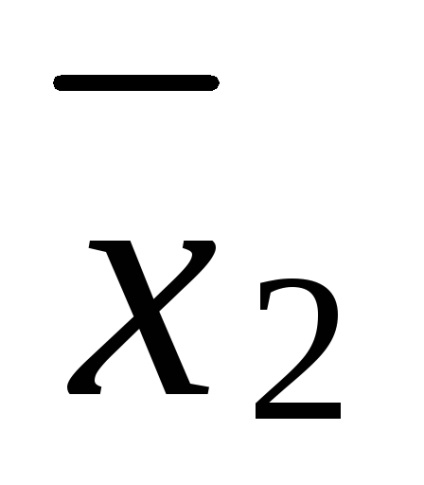
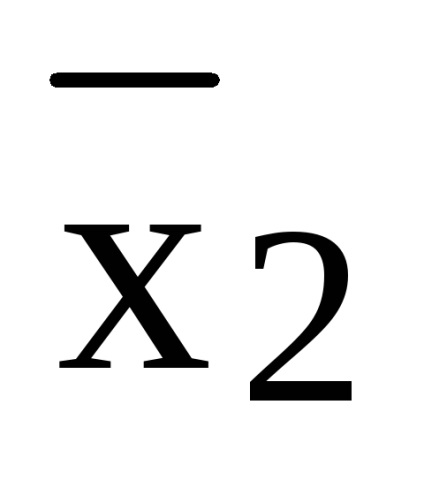
Отриманий поліном не є лінійним і має ступінь 3.
Зводиться до повної системі операцій є необхідною умовою повноти системи операцій. Необхідна і достатня умова повноти системи операцій формулюється в термінах булевих функцій.
Система булевих функцій F називається повною, якщо будь-яка функція може бути реалізована формулою над F.
Теорема Поста. Система булевих функцій сповнена тоді і тільки тоді, коли вона містить хоча б одну функцію, не зберігає 0, хоча б одну функцію, не зберігає 1, хоча б одну несамодвойственную функцію, хоча б одну немонотонну функцію і хоча б одну нелінійну функцію.
Завдання. Довести повноту системи 0. використовуючи необхідна і достатня умова повноти.
Рішення. Розглянемо відповідну 0 систему булевих функцій F0 =
Клас функцій, що зберігають 0.
Клас функцій, що зберігають 1.