Визначення. Якщо кожному значенню параметра з певного проміжку відповідає певний вектор (залежить від), то вектор називається векторною функцією (коротко вектор-функція) від скалярного аргументу і в цьому випадку пишуть:
При зміні аргументу вектор змінюється як за величиною, так і за напрямком. Надалі будемо припускати, що змінюється в проміжку, кінцевому або нескінченному.
Будемо вважати, що вектор виходить з початку координат, тобто - радіус-вектор деякої точки. В цьому випадку при зміні параметра кінець вектора опише лінію. звану годографом векторної функції. При цьому початок координат називають полюсом годографа. Рівняння (1.1) називають векторним рівнянням кривої (рис. 1.1).
Якщо у вектора змінюється тільки модуль, то годографом його буде промінь, що виходить з полюса. Якщо модуль вектора постійний і змінюється тільки його напрямок, то годограф є лінія, що лежить на сфері з центром в полюсі і радіусом, рівним модулю вектора.
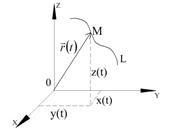
Якщо через позначити проекції вектора на осі прямокутної декартової системи координат в просторі, то ці величини для кожного значення параметра в свою чергу приймають певні числові значення і тому є скалярними функціями скалярного аргументу:
Таким чином, завдання векторної функції скалярного аргументу рівносильно завданням трьох скалярних функцій того ж аргументу. Оскільки рівняння (1.1) є рівнянням деякої кривої в просторі, то ту ж криву задають рівняння (1.2). Рівняння (1.2) - звичайні параметричні рівняння кривої в просторі.