Це зображення струмів і напруг на координатної площині через вектори, зіставлені гармонійним коливанням.
Вектори, що представляють на координатної площині гармонійні коливання різних частот, будуть обертатися проти ходу годинника навколо початку координат з різними кутовими швидкостями. Їх модулі визначаються амплітудами коливань, а кути нахилу в момент початку відліку - значеннями початкових фаз. Проекції векторів на вісь абсцис будуть являти собою косинусоидальной коливання, на вісь ординат - синусоїдальні. Вони вкажуть, як будуть змінюватися в часі миттєві значення струмів і напруг.
Малюнок 3.4 - Векторна діаграма.
Переваги: наочність інтерпретації спектрального розкладання.
Недоліки: незручність при поданні поведінки в часі напруги або струму.
Вид спектру залежить від характеру сигналу.
Розрізняють дискретні (лінійчатих) і безперервні (суцільні) спектри.
Спектр буде дискретним. якщо сигнал можна розглядати як кінцеву суму або ряд (нескінченну суму) гармонійних коливань. Він представляється на спектральної діаграмі набором окремих спектральних ліній (ліній, відповідних амплітудам і фазами гармонік).
Дискретним спектром володіють періодичні і квазіперіодичні (майже періодичні) сигнали.
Періодичними називаються сигнали, значення яких повторюються через певні рівні проміжки часу, звані періодом. Особливість спектрів періодичних сигналів полягає в тому, що частоти гармонік в них кратні основній частоті. Такі спектри називають гармонійними.
Різновидом неперіодичних сигналів є квазіперіодичні. Це сигнали, значення яких наближено повторюються через певні проміжки часу, звані майже періодом.
Малюнок 4.1 - квазипериодический сигнал.
Особливість спектрів квазипериодических сигналів полягає в тому, що частоти гармонік в них не знаходяться в кратному відношенні. Такі спектри не є гармонійними.
Малюнок 4.3 - Амплітудна спектральна діаграма ОПИ.
Спектральна щільність фаз - функція частоти, що несе інформацію про фазі елементарних гармонік.
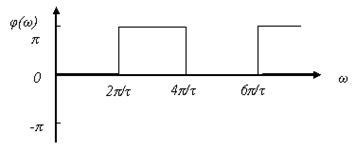
Малюнок 4.4 - Фазова спектральна діаграма ОПИ.
Розрізняють обмежені і необмежені спектри.
Обмеженим називають спектр, який має кінцевий інтервал частот, в якому розташовані всі спектральні лінії періодичного або квазіперіодичного сигналу або на якому відмінна від нуля спектральна щільність непериодического сигналу. Якщо цей інтервал нескінченний, то спектр є необмеженим
Малюнок 4.5 - Обмежений спектр.