Мал. 3.22. Векторна проекція вектора на площину.
Мал. 3.23. Векторна проекція вектора на вісь.
У векторній алгебрі часто доводиться проектувати вектор на ОСЬ, тобто на пряму, що має певну орієнтацію. Таке проектування виконується легко, якщо вектор і вісь L лежать в одній площині (рис. 3.23). Однак завдання ускладнюється, коли ця умова не виконана. Побудуємо проекцію вектора на вісь, коли вектор і вісь чи не лежать в одній площині (рис. 3.24).
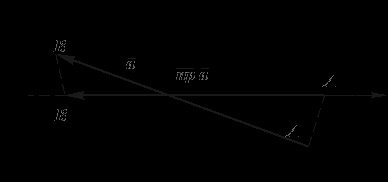
Мал. 3.24. Проектування вектора на вісь
у загальному випадку.
Доведіть, що при паралельному перенесенні векторів їх векторна проекція не зміниться.
Через кінці вектора проводимо площині, перпендикулярні прямий L. У перетині з цієї прямої дані площини визначають дві точки А1 і B1 - вектор, який будемо називати векторної проекцією даного вектора. Завдання знаходження векторної проекції може бути вирішена простіше, якщо вектор наведено в одну площину з віссю, що можливо здійснити, так як в векторній алгебрі розглядаються вільні вектори.
Поряд з векторної проекцією, існує і скалярних ПРОЕКЦІЯ, яка дорівнює модулю векторної проекції, якщо векторна проекція збігається з орієнтацією осі L, і дорівнює величині, їй протилежної, якщо векторна проекція і вісь L мають протилежну орієнтацію. Скалярну проекцію будемо позначати:
Векторна і скалярна проекції не завжди термінологічно поділяються строго на практиці. Зазвичай користуються терміном «проекція вектора», маючи на увазі під цим скалярную проекцію вектора. При вирішенні ж завдань необхідно чітко ці поняття розрізняти. Слідуючи сталій традиції, будемо використовувати терміни «проекція вектора», маючи на увазі скалярную проекцію, і «векторна проекція» - відповідно до встановленого змістом.
Доведемо теорему, що дозволяє обчислювати скалярную проекцію заданого вектора.
ТЕОРЕМА 5. Проекція вектора на вісь L дорівнює добутку його модуля на косинус кута між вектором і віссю, тобто
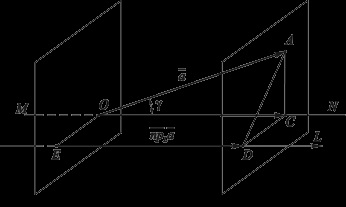
Мал. 3.25. Знаходження векторної і скалярної
Проекцій вектора на вісь L
(І вісь L однаково орієнтовані).
ДОВЕДЕННЯ. Виконаємо попередньо побудови, що дозволяють знайти кут G Між вектором і віссю L. Для цього побудуємо пряму MN, паралельну осі L і проходить через точку О - початок вектора (рис. 3.25). Кут і буде шуканим кутом. Проведемо через точки А і О дві площини, перпендикулярні осі L. Отримаємо:
Так як вісь L і пряма MN паралельні.
Виділимо два випадки взаємного розташування вектора і осі L.
1. Нехай векторна проекція і вісь L однаково орієнтовані (рис. 3.25). Тоді відповідна скалярная проекція.
2. Нехай і L орієнтовані в різні боки (рис. 3.26).
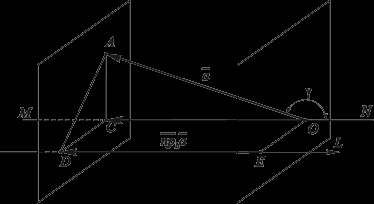
Мал. 3.26. Знаходження векторної і скалярної проекцій вектора на вісь L (і вісь L орієнтовані в протилежні сторони).
.
Таким чином, в обох випадках справедливе твердження теореми.
ТЕОРЕМА 6. Якщо початок вектора приведено до деякої точці осі L, і ця вісь розташована в площині s, вектор утворює з векторної проекцією на площину s кут, а з векторної проекцією на вісь L - кут, крім того самі векторні проекції утворюють між собою кут , то
ДОВЕДЕННЯ . Трикутники ОАВ, ОВС і ОАС - прямокутні, тому
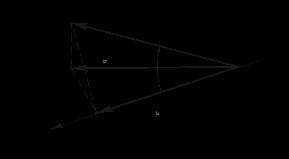
Мал. 3.27. Вектор і його векторні проекції на площину S і вісь L, що лежить в цій площині
(І вісь L однаково орієнтовані).
Сформулюйте і доведіть цю теорему, коли не всі кути A. B Обов'язково гострі (рис 3.28).
Доведена теорема важлива не тільки в векторній алгебрі, але актуальна і при вирішенні багатьох стереометричних задач.
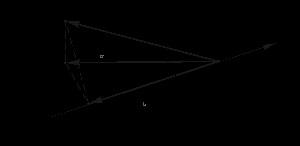
Мал. 3.28. Вектор і його векторні проекції
На площину S і вісь L, що лежить в цій площині
(І вісь L протилежно орієнтовані).