Крім змісту поняття має також обсяг.
Приклади. Обсяг поняття «стілець» включає всі стільці, обсяг поняття «стіл» - все столи.
Обсяги навіть таких простих понять, як «стілець» і «стіл», є невизначеними, розмитими, а значить, самі ці поняття відносяться до неточним. Дійсно, чи входить стілець або стіл, який тільки задумав зробити столяр, в обсяг поняття «стілець» або «стіл»? У «Ревізорі» М. В. Гоголя згадується учитель, який, розповідаючи про Олександра Македонського, так гарячкував, що ламав стільці. Чи входять ці поламані стільці в обсяг поняття «стілець»? На ці та подібні питання важко відповісти однозначно.
Між обсягами двох довільних понять, які є якийсь сенс зіставляти один з одним, має місце одне і тільки одне з наступних відносин:
підпорядкування (два варіанти)
Рівнозначними називаються два поняття, обсяги яких повністю співпадають.
Іншими словами, рівнозначні поняття відсилають до одного і того ж класу предметів, але роблять це різними способами.
Приклад. Рівнозначні поняття «квадрат» і «рівносторонній прямокутник»: кожен квадрат є рівностороннім прямокутником, і навпаки.
Рівнозначність означає збіг обсягів двох понять, але не їх змістів.
Приклад. Обсяги понять «син» і «онук» збігаються, оскільки кожен син є чийсь онук і кожен онук - чийсь син, але змісту їх різні.
Відносини між обсягами понять можна геометрично наочно представити за допомогою кругових схем. Вони називаються по імені математика XVIII століття Леонарда Ейлера (1707 - 1783) «колами Ейлера». Кожна точка кола представляє один предмет, що входить в обсяг даного поняття. Точки поза колом представляють предмети, які не підпадають під це поняття.
Відношення між двома рівнозначними поняттями зображується у вигляді двох повністю збігаються кіл.
Відносно перетину знаходяться два поняття, обсяги яких частково збігаються.
Приклад. Перетинаються обсяги понять «льотчик» і «космонавт»: деякі льотчики є космонавтами (вони представлені заштрихованої частиною кіл). Є льотчики, які не є космонавтами, і є космонавти, які не є льотчиками.
Що стосується підпорядкування перебувають поняття, обсяг одного з яких повністю входить в обсяг іншого.
Приклад. Що стосується підпорядкування перебувають імена «трикутник» і «прямокутний трикутник»: кожен прямокутний трикутник є трикутником, але не кожен трикутник - прямокутний.
Приклад. Що стосується підпорядкування перебувають поняття «дідусь» і «онук»: кожен дідусь є чийсь онук, але не кожен онук є дідусем. «Онук» - підкоряє поняття, «дідусь» - підлегле.
Якщо у відношенні підпорядкування перебувають загальні поняття, то підкоряє поняття називається родом. а підлегле - виглядом.
Приклади. Поняття «трикутник» є рід для виду «прямокутний трикутник», а поняття «онук» - рід людське око «дідусь».
У відношенні винятку перебувають поняття, обсяги яких повністю виключають один одного.
Приклади. Виключають одне одного поняття «трапеція» і «п'ятикутник», «людина» і «планета», «біле» і «червоне» і т.п.
Можна виділити два види виключення.
1. Виключають обсяги доповнюють один одного так, що в сумі дають весь обсяг роду, видами якої вони є. Поняття, обсяги яких виключають один одного, вичерпуючи обсяг родового поняття, називаються такими, що суперечать.
Приклади. Такими, що суперечать є поняття «умілий» і «невмілий», «стійкий» і «нестійкий», «гарний» і «негарний» і т.п. Суперечать один одному також поняття «червоний» і «не є червоним», вичерпні обсяг родового поняття «предмет, що має колір».
2. Виключають поняття складають в сумі лише частину обсягу того роду, видами якої вони є. Поняття, обсяги яких виключають один одного, не вичерпуючи обсяг родового поняття, називаються протилежними.
Ухвалені закони суперечать поняття Протилежні поняття
Приклади. До протилежних відносяться поняття «червоний» і «білий», не є вичерпними обсягу родового поняття «предмет, що має колір».
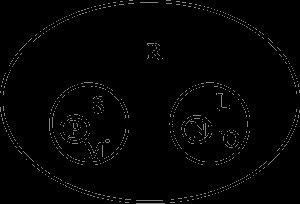
Кругові схеми можуть застосовуватися для одночасного подання об'ємних відносин більш ніж двох понять. На малюнку наводиться схема, що представляє відносини між обсягами понять:
«Планета» (S), «екзопланета» (P), «Земля» (M);
«Супутник» (L), «штучний супутник» (N), «Місяць» (O);
«Небесне тіло в Нашій Галактиці» (R).
Відповідно до цієї схеми, існують небесні тіла, які не є ні планетами, ні їх супутниками. Обсяги одиничних понять представляються точками.