Відстань між точкою і площиною визначається величиною відрізка перпендикуляра, опущеного з точки на площину.
Рішення завдання на відстань між точкою і площиною складається з послідовного виконання наступних графічних побудов
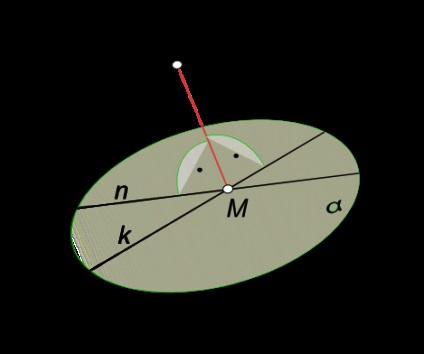
Відстань між точкою і площиною
- з точки A опустити перпендикуляр m на площину α (m ∋ A) ∧ (m ⊥ α); - знайти точку M перетину цього перпендикуляра з площиною αM = m ∩ α; - визначити дійсну величину [AM].
Якщо площину α загального положення, то для того щоб опустити на цю площину перпендикуляр, необхідно попередньо визначити напрямок проекцій горизонталі і фронталі цій площині. Знаходження точки зустрічі цього перпендикуляра з площиною також вимагає виконання додаткових графічних побудов. Рішення завдання спрощується, якщо площину α буде займати приватна положення по відношенню до площин проекцій.
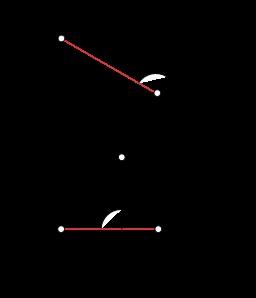
Відстань між точкою і площиною
Відстань між точкою і площиною визначається без будь-яких додаткових побудов, т. К. Площина α займає фронтально-проецирующее положення.
Відстань між точкою і площиною заданої ΔABC визначається способом зміни площин проекцій
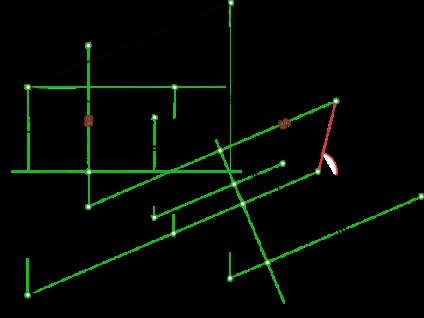
Відстань між точкою і площиною
Відстань між точкою і плоскостьюα заданої заданої слідами визначається способом зміни площин проекцій
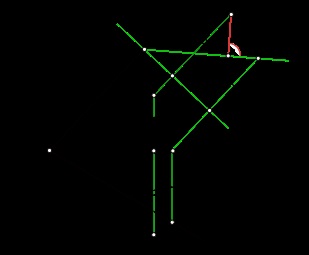
Відстань між точкою і площиною
Відстань між точкою і плоскостьюα заданої заданої ΔABC визначається класичним методом або способом прямокутного трикутника в графічній роботі 2: Графічна робота 2