1. Знайдіть матрицю, зворотну даної:
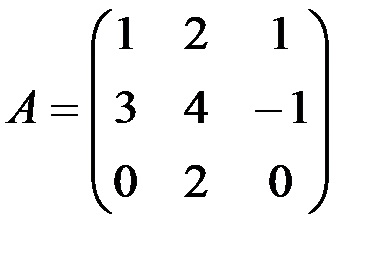
· Введіть елементи матриці в діапазон комірок А1: С3;
· Для отримання зворотного матриці виділіть несуміжний діапазон комірок такого ж розміру, наприклад E1: G3, і введіть формулу масиву. Для укладення формули в фігурні дужки після введення формули натисніть клавіші CTRL + Shift + Enter.
2. Обчисліть визначник матриці А. Для цього виділіть будь-яку вільну комірку, наприклад А5, і введіть формулу
3. Обчисліть добуток матриці А на матрицю В, де
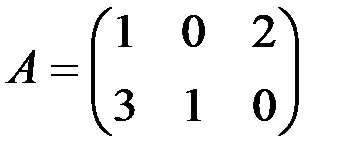
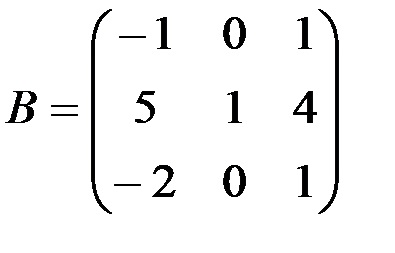
· Введіть елементи матриці А в діапазон комірок А10: С11;
· Введіть елементи матриці В у діапазон комірок А13: С15;
· Виділіть діапазон комірок з таким же числом рядків, як масив А. і з таким же числом стовпців, як масив В. наприклад, E10: G11 і введіть формулу
4. Вирішіть систему лінійних рівнянь з 3-ма невідомими
методом зворотної матриці.
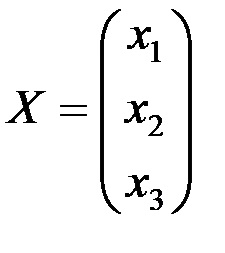
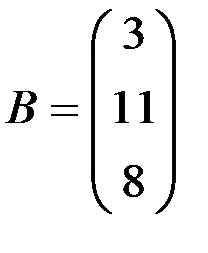
Рішення системи (1) в матричної формі має вигляд АХ = В,
де: А - матриця коефіцієнтів;
Х - стовпець невідомих;
В - стовпець вільних членів.
За умови, що квадратна матриця (2) системи (1) невироджена, тобто її визначник | А | ¹ 0, існує зворотна матриця А. Тоді рішенням системи методом зворотної матриці буде матриця-стовпець X = A B. Знайдемо це рішення. Для цього:
· Знайдемо визначник | А | = 5 (див. П. 2). Для цього активізуємо новий робочий лист і введемо елементи матриці коефіцієнтів А в діапазон комірок А1: С3. Виділимо будь-яку вільну комірку, наприклад А5, і введемо формулу
· Так як | А | ¹ 0, то матриця А - невироджена, і існує зворотна матриця А .Найдем зворотну матрицю. Для цього виділимо несуміжний діапазон комірок такого ж розміру, що і матриця А. наприклад E1: G3, і введемо формулу масиву.
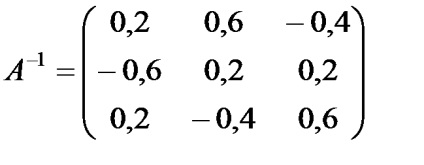
· Знайдемо рішення системи у вигляді матриці-стовпця
X = A B.. Для цього введемо елементи матриці В у діапазон комірок E6: E8, виділимо діапазон комірок з таким же числом рядків, як масив А. і з таким же числом стовпців, як масив В. наприклад, G6: G8 і введемо формулу масиву
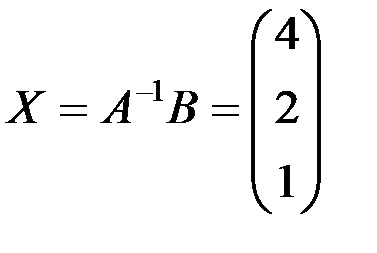
тобто рішення системи (4; 2; 1).