Мета роботи. Ознайомитися з основними характеристиками незатухаючих і затухаючих вільних механічних коливань.
Завдання. Визначити період власних коливань пружинного маятника; перевірити лінійність залежності квадрата періоду від маси; визначити жорсткість пружини; визначити період згасаючих коливань і логарифмічний декремент загасання пружинного маятника.
Прилади й приналежності. Штатив зі шкалою, пружина, набір вантажів різної маси, посудина з водою, секундомір.
1.Свободние коливання пружинного маятника. Загальні відомості
Коливаннями називаються процеси, в яких періодично змінюється одна або кілька фізичних величин, що описують ці процеси. Коливання можуть бути описані різними періодичними функціями часу. Найпростішими коливаннями є гармонічні коливання - такі коливання, при яких коливається величина (наприклад, зміщення вантажу на пружині) змінюється з часом за законом косинуса або синуса. Коливання, що виникають після дії на систему зовнішньої короткочасної сили, називаються вільними.
Розглянемо одну з найпростіших коливальних систем - пружинний маятник, який представляє собою вантаж масою m. підвішений на абсолютно пружної пружині з коефіцієнтом жорсткості k
(Рис. 1). Нехай l 0 - довжина пружини без підвішеного до неї вантажу. В разі кріплення вантажу під дією сили тяжіння пружина розтягнеться на x 1 так, що маятник буде знаходитися в положенні рівноваги внаслідок рівності модулів сили тяжіння mg і пружної сили F упр: mg = kx 1, яка прагне повернути вантаж в положення рівноваги (годиться, що деформації пружини ідеально пружні і підкоряються закону Гука).
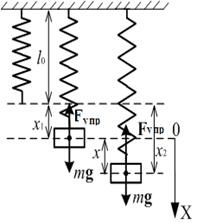
Якщо вантаж вивести з положення рівноваги, відхиливши на величину x. то сила пружності зростає: F упр = - kx 2 = -k (x 1 + x). Дійшовши до положення рівноваги, вантаж буде мати відмінну від нуля швидкістю і пройде положення рівноваги за інерцією. У міру подальшого руху буде збільшуватися відхилення від положення рівноваги, що призведе до зростання сили пружності, і процес повториться в зворотному напрямку. Таким чином, коливальний рух системи обумовлено двома причинами: 1) прагненням тіла повернутися в положенні рівноваги і 2) інерцією, яка не дозволяє тілу миттєво зупинитися в положенні рівноваги. У відсутності сил тертя коливання тривали б як завгодно довго. Наявність сили тертя призводить до того, що частина енергії коливань переходить у внутрішню енергію і коливання поступово загасають. Такі коливання називаються затухаючими.
Незатухаючі вільні коливання
Спочатку розглянемо коливання пружинного маятника, на який не діють сили тертя - незгасаючі вільні коливання. Згідно з другим законом Ньютона c урахуванням знаків проекцій на вісь X
З умови рівноваги зміщення, яке викликається силою тяжіння:. Підставляючи в рівняння (1), отримаємо:. Розділивши праву і ліву частину цього рівняння на m і приймаючи, що a = d2x / dt2. отримаємо диференціальне рівняння
Це рівняння називається диференціальним рівнянням гармонічних коливань пружинного маятника. З цього рівняння випливає, що після припинення зовнішнього впливу, що приводить до первісного відхилення системи від положення рівноваги, рух вантажу обумовлено тільки дією пружної сили (сила тяжіння викликає постійний зсув).
Загальне рішення однорідного диференціального рівняння другого порядку (2) має вигляд
Дане рівняння називається рівнянням гармонічних коливань. Найбільше відхилення вантажу від положення рівноваги А 0 називається амплітудою коливань. Величина, що стоїть в аргументі косинуса, називається фазою коливання. Постійна # 966; 0 являє собою значення фази в початковий момент часу (t = 0) і називається початковою фазою коливань. величина
є кругова або циклічна частота власних коливань. пов'язана з періодом колебанійТ співвідношенням. Період коливань визначається
Розглянемо вільні коливання пружинного маятника при наявності сили тертя (затухаючі коливання). У найпростішому і разом з тим найбільш часто зустрічається випадку сила тертя пропорційна швидкості # 965; руху:
де r - постійна, яка називається коефіцієнтом опору. Знак мінус показує, що сила тертя і швидкість мають протилежні напрямки. Рівняння другого закону Ньютона в проекції на вісь Х при наявності пружної сили і сили тертя
Дане диференціальне рівняння з урахуванням # 965; = dx / dt можна записати
де - коефіцієнт загасання; - циклічна частота вільних незгасаючих коливань даної коливальної системи, т. Е. При відсутності втрат енергії (# 946; = 0). Рівняння (8) називають диференціальним рівнянням згасаючих коливань.
Щоб отримати залежність зміщення x від часу t. необхідно вирішити диференціальне рівняння (8). У разі малих затуханий () рішення рівняння можна записати в такий спосіб:
де А 0 і # 966; 0 - початкова амплітуда і початкова фаза коливань;
- циклічна частота згасаючих коливань при # 969; >> # 969; ≈ # 969; 0.
Рух вантажу в цьому випадку можна розглядати як гармонійне коливання з частотою # 969; і змінною амплітудою, мінливої по закону:
На графіку функції (9), рис. 2, пунктирними лініями показано зміна амплітуди (10) згасаючих коливань.
Мал. 2. Залежність зміщення х вантажу від часу t при наявності сили тертя
Для кількісної характеристики ступеня загасання коливань вводять величину, рівну відношенню амплітуд, що відрізняються на період, і звану декрементом загасання:
Часто використовують натуральний логарифм цієї величини. Такий параметр називається логарифмічним декрементом загасання:
Якщо за час t 'амплітуда зменшується в n раз, то з рівняння (10) випливає, що
Звідси для логарифмічного декремента отримуємо вираз
Якщо за час t 'амплітуда зменшується в е раз (е = 2,71 - основа натурального логарифма), то система встигне зробити число коливань
Отже, логарифмічний декремент загасання - величина, зворотна числу коливань, що здійснюються за той час, за яке амплітуда зменшується в е раз. Чим більше # 952 ;, тим швидше відбувається загасання коливань.
2. Методика експерименту і експериментальна установка
Мал. 3. Схема установки
Установка складається з штатива 1 з вимірювальною шкалою 2. До штатива на пружині 3 підвішуються вантажі 4 різної маси. При вивченні згасаючих коливань в завданні 2 для посилення загасання використовується кільце 5. яке поміщається в прозору судину 6 з водою.
У завданні 1 (виконується без судини з водою і кільця) в першому наближенні загасанням коливань можна знехтувати і вважати гармонійними. Як випливає з формули (5) для гармонійних коливань залежність T 2 = f (m) - лінійна, з якої можна визначити коефіцієнт жорсткості пружини k за формулою
де - кутовий коефіцієнт нахилу прямої T 2 від m.
Завдання 1. Визначення залежності періоду власних коливань пружинного маятника від маси вантажу.
1. Визначити період коливань пружинного маятника при різних значеннях маси вантажу m. Для цього за допомогою секундоміра для кожного значення m тричі виміряти час t повних n коливань (n ≥10) і за середнім значенням часу обчислити період. Результати занести в табл. 1.
2. За результатами вимірювань побудувати графік залежності квадрата періоду T2 від маси m. З кутового коефіцієнта графіка визначити жорсткість пружини k за формулою (16).
Результати вимірювань для визначення періоду власних коливань
3. Додаткове завдання. Оцінити випадкову, повну і відносну # 949; t помилки вимірювання часу для значення маси m = 400 г.
Завдання 2. Визначення логарифмічного декремента загасання пружинного маятника.
1. На пружину підвісити вантаж масою m = 400 г з кільцем і помістити в посудину з водою, так щоб кільце повністю перебувало в воді. Визначити період згасаючих коливань для даного значення m за методикою викладеною в п. 1 завдання 1. Вимірювання повторити три рази і результати занести в ліву частину табл. 2.
2. Вивести маятник з положення рівноваги і, зазначивши по лінійці його початкову амплітуду, виміряти час t '. протягом якого амплітуда коливань зменшується в 2 рази. Вимірювання провести три рази. Результати занести в праву частину табл. 2.
3. Розрахувати за формулою (14) логарифмічний декремент загасання # 952 ;, враховуючи, що ln2 = 0,693.
для визначення логарифмічного декремента загасання
Вимірювання періоду коливань
зменшення амплітуди в 2 рази
4. Контрольні питання і завдання
1. Які коливання називаються гармонійними? Дайте визначення їх основних характеристик.
2. Які коливання називаються затухаючими? Дайте визначення їх основних характеристик.
3. Поясніть фізичний зміст логарифмічного декремента загасання і коефіцієнта загасання.
4. Вивести залежності від часу швидкості і прискорення вантажу на пружині, що здійснює гармонійні коливання. Привести графіки і проаналізувати.
5. Вивести залежності від часу кінетичної, потенційної і повної енергії для вантажу, що коливається на пружині. Привести графіки і проаналізувати.
6. Отримати диференціальне рівняння вільних коливань і його рішення.
7. Побудувати графіки гармонійних коливань з початковими фазами π / 2 і π / 3.
8. У яких межах може змінюватися логарифмічний декремент загасання?
9. Привести диференціальне рівняння затухаючих коливань пружинного маятника і його рішення.
10. За яким законом змінюється амплітуда згасаючих коливань? Чи є затухаючі коливання періодичними?
11. Який рух називається апериодическим? За яких умов воно спостерігається?
12. Що називається власною частотою коливань? Як вона залежить від маси тіла, що коливається для пружинного маятника?
13. Чому частота згасаючих коливань менше частоти власних коливань системи?
14. Підвішений до пружини мідна кулька здійснює вертикальні коливання. Як зміниться період коливань, якщо до пружини підвісити замість мідного кульки алюмінієвий того ж радіуса?
15. При якому значенні логарифмічного декремента загасання коливання загасають швидше: при # 952; 1 = 0,25 або # 952; 2 = 0,5? Привести графіки цих згасаючих коливань.
3. Ахматов А. С. Лабораторний практикум з фізики /.
- М. Вища. шк. 1980. - 359 с.