Коливальні процеси, з якими доводиться зустрічатися, підрозділяють на періодичні і неперіодичні в залежності від характеру зміни з часом фізичних величин, що характеризують стан системи. Через свого виникнення коливання підрозділяють на вільні та вимушені.
Вільними (власними) коливаннями називаються коливання, які виникають в системі в результаті однократного початкового виведення її зі стану стійкої рівноваги. При вільних коливаннях в системі завжди діють сили (в загальному випадку причини), які прагнуть повернути систему в положення рівноваги. (В разі коливання вантажу на пружині повертає силою буде сила пружності пружини.)
Якщо в системі відсутні сили тертя і будь-які інші причини, що перешкоджають вільним коливанням, то немає втрат механічної енергії, і коливання можуть відбуватися як завгодно довго з постійною амплітудою. Такі вільні коливання називаються незатухающими. Незгасаючі коливання являють ідеалізований випадок коливань. Вільні коливання реальних систем завжди затухаючі. Загасання коливань пов'язано, головним чином, з дією в системі сил тертя. Незгасаючі коливання в реальній системі можуть порушуватись впливом на неї змінної зовнішньої сили. У цьому випадку коливання називаються змушеними.
Періодичними називають коливання, при яких значення всіх фізичних величин, що змінюються в процесі коливань, повторюються через рівні проміжки часу. Найменший такий проміжок часу, після закінчення, якого повторюються значення всіх величин, що характеризують коливальний рух, називається періодом коливань. За цей час, кажуть, відбувається одне коливання.
Частотою періодичних коливань називають число коливань в одиницю часу. Якщо за час система здійснює коливань, то частота коливань дорівнює:. З огляду на, що за час, що дорівнює періоду відбувається одне коливання, приходимо до зв'язку частоти з періодом:
Частоту вимірюють в герцах (Гц). За 1 Гц приймають частоту такого коливального процесу, при якому за одну секунду відбувається одне повне коливання (Гц = 1 / с).
Окремим випадком періодичних коливань є гармонійні коливання, в яких коливається фізична величина (наприклад, координата вантажу на пружині) змінюється з часом за законом косинуса (або синуса):
де величина, рівна найбільшому абсолютним значенням величини, що коливається, називаються амплітудою коливань. Вираз визначає значення в будь-який момент часу і називається фазою коливання. У початковий момент часу фаза дорівнює початковій фазі.
Величину називають циклічною частотою гармонійного коливання.
Періодом функції (1), як відомо з математики, є
- це і буде період коливань. Для частоти гармонійного коливання маємо:
Зауважимо, що функція (1) є рішенням диференціального рівняння:
де - друга похідна функції за часом.
;
і при підстановці в рівняння (2) воно звертається в правильне рівність, що й треба було довести.
В математиці доводиться, що функція (1) є єдиним рішенням диференціального рівняння (2). Таким чином, якщо при коливаннях для хитається фізичної величини в будь-який момент часу має місце співвідношення (2). то коливання є гармонійними і відбуваються з періодом
Значення постійних і визначаються, як правило, з початкових умов.
У лабораторній роботі 2 Вам належить експериментально дослідити вільні коливання пружинного і математичного маятників.
Пружинний маятник. Методика експерименту
Пружинним маятником називають тіло, підвішене на пружині. Нехай на пружині жорсткістю підвішений вантаж масою (рис.1)
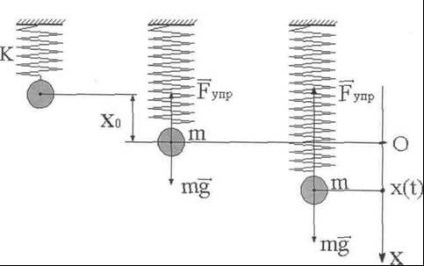
Розглянемо вертикальний рух вантажу, яке буде відбуватися після невеликого поштовху під дією сили пружності пружини і сили тяжіння. Пружину припускаємо легкої і її масою нехтуємо. Також нехтуємо силою опору повітря, вважаючи її малою.
Хитається фізичною величиною в даному прикладі є координата вантажу. Помістимо початок відліку по осі в точку, відповідну рівноважного стану вантажу (рис.1). У цьому положенні пружина вже розтягнута на величину, яка визначається з умови рівноваги
При зміщенні вантажу з положення рівноваги, наприклад вниз, на відстань, на нього крім сили тяжіння
діє сила пружності, рівна відповідно до закону Гука так, як показано ні рис.1.
Запишемо рівняння другого закону Ньютона для вантажу в проекції на вісь:
З урахуванням співвідношення (3) рівняння другого закону Ньютона наводиться до виду
де проекція прискорення на вісь є не що інше, як друга похідна за часом від координати вантажу, тобто . Таким чином, ми отримаємо, що в довільний момент часу при коливаннях вантажу для його координати має місце співвідношення
Отже, розглянуті коливання є гармонійними і відбуваються з циклічною частотою
В ході експерименту ви повинні переконатися, що період не залежить від амплітуди коливань вантажу і за вимірюваним періоду коливань і відомим значенням маси вантажу розрахувати жорсткість пружини відповідно до співвідношення (5) за формулою
Визначити жорсткість пружини можна і іншим методом. Для цього треба виміряти деформацію пружини в положенні рівноваги вантажу і скористатися рівнянням (3), згідно з яким
Після оцінки похибок, отримані значення слід зіставити один з одним і пояснити, в разі необхідності, причини можливої невідповідності.