Для вимірювання імпедансу датчиків і його параметрів-ак-тивного і реактивних опорів і відповідно R, L і С-використовують мости змінного струму.
Електричну схему заміщення датчика, що характеризується опором, можна уявити двополюсників з послідовно-них або паралельним з'єднанням активного і реактив-них опорів, як це показано на рис 3.19. Основні з-відносини, якими характеризуються двухполюсники, приве-ку на рис. 3.19, а і 3.19,6. Та чи інша схема заміщення ви-вибирається залежно від виду розсіюється (втрачається) мощ-ності «а елементах двухполюсника. Якщо ці втрати пропорції-нально квадрату протікає через двухполюсник струму I, що має місце при наявності переважаючого активного опору-лення проводу котушки індуктивності або витоку струму через конденсатор, т. Е. Втрачається активна потужність на нагрів котушки або конденсатора, то датчик заміщають послідовними схемами. Якщо втрати пропорційні квадрату напруги на двухполюсника, що має місце в разі діелектричних втрат в конденсаторі або великий індуктивності котушки (втрати реактивної потужності), то вибирають паралельну схе-му заміщення.
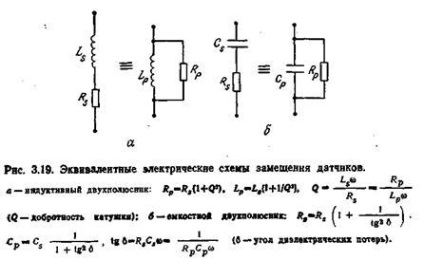
Вимірювання параметрів ємнісного датчика. Діелектричні потерн в конденсаторі можна уявити резистором з опору-опором Rc включеним паралельно з конденсатором їм-кісткою СC.
Принципова схема вимірювань з датчиком місткості є так званий міст Нернста (рис 3.20). Імпеданс датчика дорівнює
імпеданс врівноважує плеча визначається виразом
Умова рівноваги моста:, тобто н. Міст врівноважують при значенні вимірюваної ве-личини то, прийнятому за початкове. Коли т0 змінює-ся на. імпеданс датчика
змінюється від Zc o до. Тоді між точками А і В у діагоналі моста з'являється напруга розбалансу
і якщо . то з точністю до малих другого по-рядка
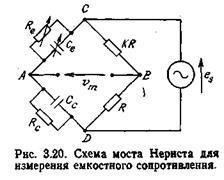
Вибираючи. K = 1, отримують максимальну чутливість схе-ми. Крім того, завдяки симетрії моста легше скомпенсі-ровать вплив впливають величин. При цих умовах
Якщо датчик являє собою конденсатор з повітряним ді-електриком, то втрати пренебрежимо малі, і імпеданс датчика носить ємнісний характер. У цьому випадку резистор Rе для рівнян-новешіванія моста можна не використовувати. В такому мосту, через відоме як міст Сауті (рис. 3.21), напруга розбалансу одно
Міст врівноважують при значенні те, що приймається за на-чільного значення вимірюваної величини. і встановлюють Се = Сс о. тоді при
Якщо з точністю до малих
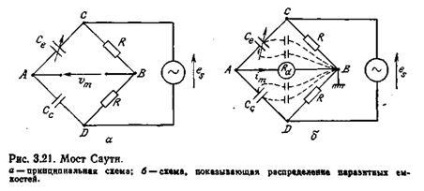
Обкладки конденсаторів утворюють з масою паразитні їм-кістки, розподілені як показано на рис. 3.21,6. Ці пара-зітние конденсатори паралельні кожному з резисторів R і вхідного імпедансу вимірювального приладу з активним со-спротивом Rd. Їх вплив на плечі моста можна зро-лать дуже незначним вибором вельми малих опираючись-ний R (10 2 --10 3 Ом) в порівнянні з паразитних ємнісним опором. Більш зручним є включення паралель-но кожному резистору конденсатора невеликої ємності, що дозволяє врівноважити міст компенсацією паразитних ємко-стей.
Паразитне ємнісний опір, паралельне вхідного ланцюга вимірювального приладу, не впливає на рівновагу моста, але воно може впливати на чутливість схеми до разбалансу, якщо це паразитное ємнісний опір не надто вели-ко в порівнянні з вхідним імпедансом вимірювального приладу. У цьому випадку більш розумно проводити вимірювання струму разбаланса, використовуючи вимірювальний прилад з вхідним импе-данс, набагато меншим, ніж підключений йому в паралель паразитное ємнісний опір.
Струм разбаланса моста Сауті, коли вхідний імпеданс изме-рительного приладу дуже малий, визначається висловлю-ням
В легко реалізується випадку, коли
Вимірювання параметрів індуктивного датчика. Залежно від того, як краще представити втрати в котушці датчика - послідовним або паралельним опором відпо-відної схеми заміщення, використовують відповідно міст Максвелла (рис. 3.22, а) або міст Гея (рис. 3.22, б).
Умова рівноваги для обох мостових схем одне і те ж:
Для моста Максвелла
а для моста Гея
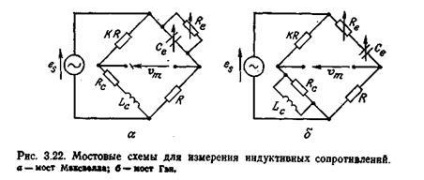
Опір і індуктивність датчика в функція значень параметрів елементів моста визначаються в обох мостових схемах як
Напруга розбалансу в обох схемах визначається Вира-ням
і якщо \ Z \<<\KR+Zc o\, то с точностью до малых второго по-рядка
Чутливість зазначених мостових схем максимальна при | Zc0 | = KR, і, приймаючи .K = 1 і R = | Zc0 |, отримаємо
Якщо два датчика з однаковими статичними Імпеданс поміщаються в суміжні галузі моста, утворюючи диференціальну схему, то в результаті забезпечується компенсація віз-дії впливають величин. І так як варіації вимірюваної величини викликають ідентичні за значеннями, але протипожежні-помилкові по знаку реакції датчиків, то досягаються поліпшення лінійності характеристики перетворення схеми в цілому і линеаризация сукупної характеристики датчиків зокрема.
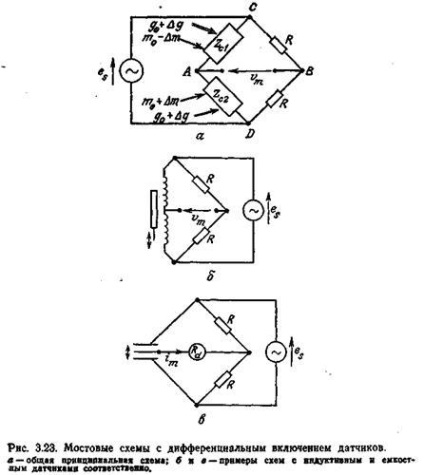
Принципові схеми мостів з диференціальним вклю-ням індуктивних датчиків наведені на рис. 3.23. Напругу разбаланса в функції импедансов датчиків Zc1 і Zc2 виражається співвідношенням
Tax як при впливі вимірюваної величини
Коли впливає величина викликає однакові зміни імпедаісов Zc1. і Zc2, а вимірювана величина - їм взаємодоповнюючі, то можна записати, що
де Sg - чутливість до впливає величиною, а S -чувст-вітельность до вимірюваній величині. З огляду на це попе-ний вираз для напруги розбалансу можна записати у вигляді
Таким чином, напруга розбалансу є лінійна функція збільшень вимірюваної величини; при цьому вплив впливав-нього величини зменшено. Якщо збільшення імпедансу дат-чика, викликані впливає величиною, малі в порівнянні зі статичним опором Zc0. що зазвичай має місце, то
У разі, коли характеристики датчиків нелінійні і нелінійної-ність, наприклад, квадратична, рівні і протилежно на-правління впливу вимірюваної величини викликають изме-нения импедансов датчиків, які вже не є однаковий-вимі за величиною і протилежними за знаком, т. Е .
Напруга розбалансу в цьому випадку виражається нелінійної-ним співвідношенням
Яке, приводиться до лінійного вигляду
якщо. що зазвичай має місце.