У різних фізичних явищах і виробничих процесах деякі величини змінюються, а інші зберігають своє числове значення. Наприклад, при роботі токарного верстата час, відстань переміщення супорта змінюються (змінні величини зазвичай позначаються x, y, z), а швидкість обертання деталі залишається умовно-постійної (будемо такі величини позначати - a, b, c). Але, як відомо, абсолютних констант в природі дуже мало. Спостережувані в техніці параметри виробничих процесів і характеристики якості, що відносяться як до названих вище змінним, так і до умовно-постійних величин, є випадковими величинами.
Випадковою величиною називається величина, яка в результаті випробувань або контролю може прийняти те чи інше значення в межах певного інтервалу.
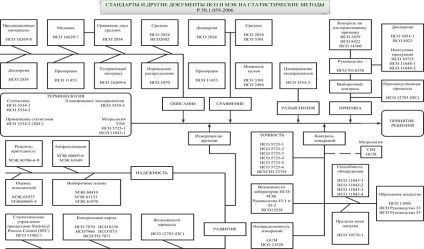
Наприклад, дійсний розмір обробленої деталі є випадковою величиною, так як він може прийняти будь-яке числове значення в певних межах. За ролі в дослідженні вони класифікуються на залежні і незалежні (рис. 1.2).
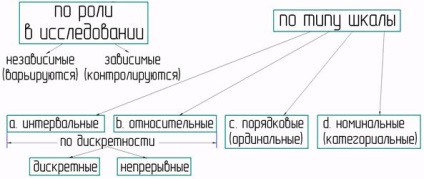
Мал. 1.2 Класифікація випадкових величин
Незалежними випадковими величинами (факторами, також «пояснюють», «екзогенними» випадковими величинами або «предикторами», xi) називаються випадкові величини, які варіюються дослідником.
Прімерамінезавісімих випадкових величин можуть бути:
- швидкість обертання шпинделя,
- подача супорта верстата,
- використовувана мастильно-охолоджуюча рідина,
- марка матеріалу, конструкція або інша характеристика інструменту і т. д.
Незалежні випадкові величини залежать тільки від експериментатора, який маніпулює ними, впливаючи на "залежні випадкові величини".
Зовсім випадкові величини (звані також «ендогенними» або «відгуками», yi) вимірюються або реєструються і є зазвичай предметом оптимізації
В якості останніх можуть бути робота, технічні характеристики якості, економічні показники і т.д. Інакше, залежність проявляється в реакції досліджуваного об'єкта на вплив.
Типи випадкових величин. Залежно від використовуваної шкали вимірювань, як правило, випадкові величини поділяють на чотири основні типи (див. Рис. 1.2):
b. Порядкові (ординальні) випадкові величини дозволяють ранжувати (упорядкувати) об'єкти, вказавши які з них в більшій чи меншій мірі володіють якістю, вираженим даної випадкової величиною. Однак вони не дозволяють сказати "на скільки більше" або "на скільки менше". Наприклад, можна випадкову величину, яка має вік (хлопчик - юнак - чоловік - старий), оцінювати в балах. Таким же чином в балах можна оцінювати знання студентів, якість деталі, придатність технологічного процесу.
c. Інтервальні випадкові величини дозволяють не тільки впорядковувати об'єкти вимірювання, але і чисельно висловити і порівняти відмінності між ними. Наприклад, температура, виміряна в градусах Фаренгейта або Цельсія, розмір деталі, шорсткість її поверхні характеризуються «в інтервального шкалою». Можна, наприклад, сказати, що температура 40 Про З вище, ніж температура 30 Про С на 10 градусів.
d. Відносні випадкові величини дуже схожі на інтервальні випадкові величини. На додаток до всіх властивостей випадкових величин, виміряних в інтервального шкалою, їх характерною рисою є наявність певної точки абсолютного нуля. Прикладом відносної випадкової величини є температура, виражена за шкалою Кельвіна. Стосовно до цих випадкових величин можна оцінювати у скільки разів одна величина більше або менше іншого. Тобто допустимо вираз типу: 40 Про До в два рази більше, ніж 20 Про К. Інтервальні шкали, наприклад, шкала Цельсія даними властивістю не володіють. Слід зауважити, що в більшості статистичних процедур не робиться відмінності між властивостями інтервальних шкал і шкал відносини.
Інтервальні та відносні випадкові величини можуть бути дискретними і безперервними (див. Рис. 1.2).
Дискретної випадкової величиною називається така величина, які при-ють окремі, здебільшого цілочисельні значення.
Безперервною випадковою величиною називається така величина, яка може приймати будь-які числові значення з інтервалу можливих значень.
Напри-заходів, число деталей, оброблених на верстаті, є дискретна випадкова величина, а розмір деталі - безперервна випадкова величина. (Іноді використовується поняття «змішаної випадкової величини», яка визначається наявністю декількох безперервних інтервалів можливих значень, розділених проміжками).
За тимчасової приналежності випадкові величини зазвичай діляться на два види: перехресні дані (cross-section data) і тимчасові ряди (time series).
Перехресні дані - визначають значення показників, що відносяться до одного моменту часу, або значення показників, тимчасова приналежність яких не така істотна. Наприклад, при дослідженні залежності шорсткості поверхні від складу МОР, якщо порівнюються середні значення шорсткості деталей, оброблених в різних МОР, час і порядок обробки деталей неважливі.
Часовий ряд. ряд динаміки, динамічний ряд - послідовність чисел, елементи якої ( «рівні ряду») - значення статистичного показника (ознаки), що протікає в часі процесу. Наприклад, досліджується зміна шорсткості поверхні при обробці з плином часу за рахунок зміни складу і властивостей МОР, геометрії ріжучої кромки інструменту і т.д. Тут час або порядок обробки деталей мають вирішальне значення. (Детальніше тимчасові ряди розглянуті в гл. 8).