Рівняння коливання точки має наступний вигляд х = Asin (wt + фі (0)). Тут А - амплітуда коливань, w - частота коливань і фі (0) - початкова фаза коливань. На жаль в БВ не можна використовувати грецькі літери, тому замість омега я написав w і замість грецької букви фі так і написав по-російськи фі. Початкова фаза коливань дорівнює нулю, тобто фі (0) = 0. Тоді рівняння наших застережень таким
У початковий момент часу при t = 0 маємо Asin (wt) = 0, тоді х (0) = 0. Я вже забув, в якому класі проходять похідні. Для того щоб знайти рівняння для швидкості коливань v, треба взяти похідну по часу з рівняння (1). отримаємо
У початковий момент часу (t = 0), cos (wt) = 1. Швидкість коливань буде максимальною і рівною v (макс) = wA. Один період коливань = 2Пі, де пі = 3,14 - це грецька буква пі.
Період коливань зазвичай позначається буквою Т. Маємо Wт = 2Пі. Або період Т = 2Пі / w. У задачі сказано, коли швидкість точки стане дорівнює половині максимальної швидкості. Тобто v = v (макс) / 2 = wA / 2 = 0,5wA. З рівняння 2 треба знайти цей час t. маємо
0,5wA = wAcos (wt). Звідси знаходимо cos (wt) = 0,5. Косинус дорівнює 0,5 (або 1/2), коли wt = пі / 3. Це вже з тригонометрії. Знаходимо t = пі / 3w. Але w = 2Пі / Т. тоді маємо
t = пі / 3w = Піт / (3 * 2Пі) = Т / 6, де * - знак множення. Відповідь: швидкість хитається точки дорівнюватиме половині її максимальної швидкості при Т / 6, тобто 1/6 від періоду коливань.
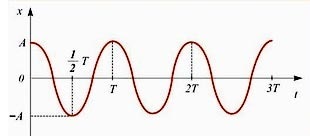
А це графік гармонічних коливань
А тут представлений графік зміни швидкості з часом. Тут по вертикалі треба відкласти швидкість v, а не х. І амплітуда дорівнює wA, а не А.