МІНІСТЕРСТВО ОСВІТИ РФ
Державна освітня установа
ВИЩОЇ ОСВІТИ
«ЛИПЕЦЬКА державний технічний університет»
Кафедра прикладної математики
по курсу «Економіко-математичні методи і моделі»
на тему «Визначення координат розташування двох складів в регіоні»
РОЗТАШУВАННЯ ПОСТАЧАЛЬНИКІВ І КЛІЄНТІВ
ВИЗНАЧЕННЯ КООРДИНАТ ПЕРШОГО СКЛАДУ
ВИЗНАЧЕННЯ КООРДИНАТ ДРУГОГО СКЛАДУ
Список використаних джерел
Переміщення матеріальних потоків в логістичному ланцюзі практично неможливо без їх концентрації на складах. Ціна товару в значній мірі залежить від витрат, зв'язкових із складуванням розподіляється продукції і з відстанню, методами і засобами доставки товару від складу до споживача. В наслідок з цим велике значення має завдання оптимізації розміщення розподільного складу. В ідеалі він повинен бути розташований таким чином, щоб сумарні витрати, пов'язані з доставкою товарів споживачам, були мінімальні.
У даній роботі розглянуто визначення координат оптимального розташування двох складів мінеральної води в місті Липецьку.
РОЗТАШУВАННЯ ПОСТАЧАЛЬНИКІВ І КЛІЄНТІВ
Розташування постачальників (виробників) і клієнтів (споживачів) мінеральної води визначимо за допомогою «Липецький інформаційної системи» (ЛИС). Масштаб виберемо як показано на малюнку 1. Осями координат будуть краю видимої частини карти міста. Лівий край - вісь Y, нижній - вісь X. Всі точки постачальників і клієнтів прономеруем.
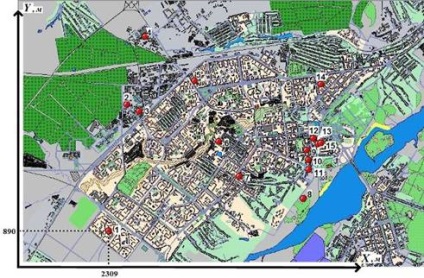
Малюнок 1 - Розташування постачальників і клієнтів
У підсумку отримуємо координати виробників і споживачів, представлені в таблиці 1.
Таблиця 1 - Координати постачальників і клієнтів
Відстань між об'єктами визначимо як корінь квадратний із суми квадратів різниць їх координат. Введемо умова зразкового рівності складів, щоб завдання не стала многокритериальной.
У роботі розглянемо ітераційний алгоритм пошуку складів. Виберемо еврестіческі координати першого і другого складів, потім вирішимо транспортну задачу за допомогою Excel модулем «Пошук рішення». Потім будемо міняти координати тільки одного складу і виберемо варіант де загальна відстань від постачальників і споживачів буде мінімальним (Розрахунки здійснюємо в Excel). Коли знайдемо ці оптимальні координати першого складу, зафіксуємо їх і приступимо до пошуку координат другого складу, таким же чином.
ВИЗНАЧЕННЯ КООРДИНАТ ПЕРШОГО СКЛАДУ
Вибираємо координати складів еврестіческім методом, тобто інтуїтивно. Перший візьмемо так: (3750; 3200), а другий - (7550; 3115).
З використанням Excel, знаходимо відстані від постачальників до першого і другого складів (таблиця 4).
Таблиця 4 - Відстані від постачальників до першого і другого складів
У модулі «Пошук рішення» встановлюємо цільову осередок рівну мінімальному значенню і відповідні обмеження (малюнок 2). Як формули цільової функції будемо використовувати функцію «СУММПРОИЗВ», яка перемножує відповідні елементи заданих масивів і повертає суму творів.
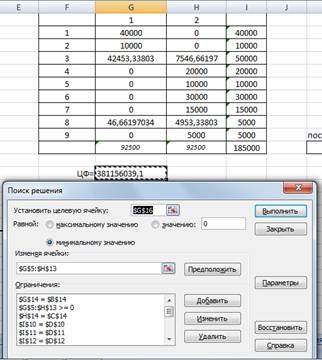
Малюнок 2 - Пошук значення цільової функції
На даному етапі отримуємо значення цільової функції, яке відповідає загальному відстані поставок мінеральної води на склади.
Щоб визначити мінімальну відстань від складів до постачальників введемо додаткову таблицю, заповнену нулями і одиницями. Одиниця відповідає нульове значення таблиці, зображеної зліва на малюнку 3, а нуль ставиться, якщо в лівій таблиці у відповідній клітинці стоїть нуль.
За допомогою функції «СУММПРОИЗВ» знайдемо мінімальну відстань від постачальників до складів, перемноживши значення з таблиці 4 і додаткової таблиці, зображеної зліва на малюнку 3.
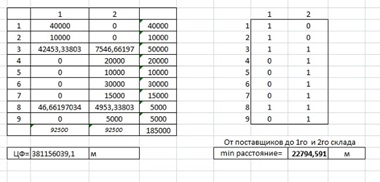
Малюнок 3 - Визначення мінімальної відстані від постачальників до складів
Отримуємо, що мінімальна відстань від постачальників до складів, з вибраними координатами, становить 22794,591 метрів.
Далі також за допомогою Excel, знаходимо відстані від клієнтів до першого і другого складів (таблиця 5).
Таблиця 5 - Відстані від клієнтів до першого і другого складів
За допомогою модуля «Пошук рішення» проробляємо ті ж дії, що описані вище для постачальників і отримуємо мінімальну відстань від клієнтів до складів, рівне 12618,08 метрів (рисунок 4).
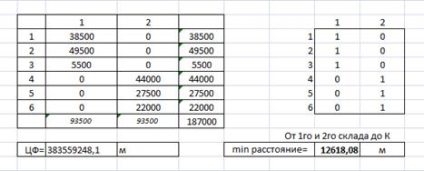
Малюнок 4 - Визначення мінімальної відстані від клієнтів до складів
І останнім кроком на даній ітерації буде визначення загального мінімальної відстані, шляхом складання мінімальної відстані від клієнтів до складів і мінімальної відстані від постачальників до складів:
.
Таким чином отримали, що від складів з координатами (3750; 3200) і (7550; 3115) мінімальна відстань до постачальників і клієнтів дорівнюватиме
.
За допомогою ЛИС дивимося, як можна поміняти координати першого складу, де його розташувати, і міняємо попередні координати першого складу на (3333; 3355). Другий склад залишаємо на тому ж місці.
У табличному процесорі MS Excel повторюємо дії першої ітерації і знаходимо мінімальну відстань від постачальників і клієнтів до складів рівне
.
Як видно, при таких координатах першого складу, загальна відстань збільшилася, значить необхідно на наступній ітерації шукати розташування складу в іншому напрямку.
Таким чином будемо міняти координати першого складу і порівнювати загальне відстань. В результаті виберемо мінімальне.
Подальші ітерації наведені в таблиці 6.
Таблиця 6 - Розрахунки мінімального відстані
Після проведення 17 ітерацій по карті ЛИС стало видно, що немає необхідності в подальших пошуках, знайдені оптимальні координати першого складу (4356; 3430) і другого (7360; 3171).
Оптимальне розташування двох складів мінеральної води в Липецьку знайдено. Перший склад має координати (4356; 3430), другий - (7360; 3171). вони представлені на малюнку 5 червоними кружками. Розташувавши склади в даних точках, витрати на первозки продукції будуть мінімальними.
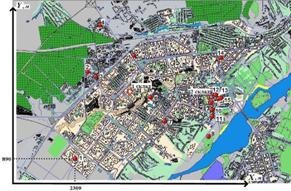
Малюнок 5 - Оптимальне розташування двох складів в регіоні
У даній роботі за допомогою табличного процесора Excel було знайдено оптимальне розташування двох складів мінеральної води в місті Липецьку. Перебір координат складів проводився еврестіческім методом, з отриманих результатів вибирався той, де загальна відстань від постачальників і клієнтів було мінімальним. Розмістивши склади в знайдених точках, витрати на первозки мінеральної води будуть мінімальними.
Список використаних джерел