Визначення максимального обсягу коробки
I етап. Постановка задачі
Є квадратний аркуш картону зі стороною а. З листа роблять коробку наступним чином: по кутах вирізують чотири квадрата і склеюють коробку по сторонам вирізів.
Визначити, яка повинна бути сторона вирізуваного квадрата, щоб коробка мала найбільшу місткість.
У задачі розглядається процес перетворення одного об'єкта (картонного листа) в інший (коробку). Вихідний об'єкт - картонний лист - має задані геометричні розміри: довжина сторони а. Створений об'єкт - коробка - характеризується обсягом, а вирізи - розміром сторони і площею.
II етап. Розробка моделі
Об'єкт "картонний лист" має керовані параметри.
-
Довжина сторони а; Довжина вирізу b.
Дії над об'єктом.
-
Вирізання квадратних областей по краях; Склеювання сторін вирізів.
Об'єкт "коробка" має керовані параметри.
-
Довжина сторони c; Площа дна S; Обсяг V.
Дії над об'єктом.
-
Розрахунок площі та об'єму.
-
c = a - 2b - довжина сторони дна; S = c2 - площа дна; V = Sb - обсяг.
Тут a - довжина сторони картонного листа, b - довжина вирізу.
Для моделювання використовуємо середу електронної таблиці, в якій інформаційна та математична моделі об'єднуються в таблицю, яка має три області:
-
вихідні дані - керовані параметри; проміжні розрахунки; результати
Довжина вирізу від 1 до 20
ПЕРЕД формулі завжди СТАВИТЬСЯ ЗНАК =
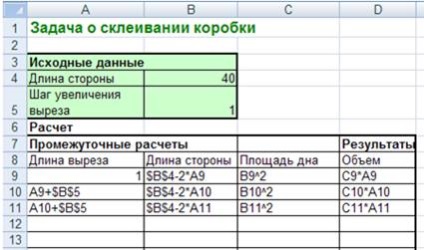
Таблиця після введення всіх формул
Завдання про склеюванні коробки