Жодна страва не обходиться без ріпчастої цибулі. Вирощують його самостійно багато людей. Окультурено ця рослина була дуже і дуже дано. Експедиція Христофора.
З сепарованого продукту феромагнітні тіла витягують за допомогою Железоотделители. Потужне магнітне поле допомагає в цьому. Матеріал на конвеєрі під час руху.
Кукурудза - універсальна і відрізняється високою продуктивністю злакова культура. Вирощують її для вживання молодих качанів, на корм птиці та тварин, для.
Для мусульман термін «Халяльная їжа» означає в основному вірність традиціями. Заборонені до вживання компоненти в таких продуктах повинні бути відсутніми, якщо.
Бажаного врожаю посіви кукурудзи не принесуть, якщо хвороби або шкідники зашкодять саджанці. Розпізнавати основні захворювання потрібно вміти, як і боротися з ними.
-
hleb-produkt.ru »Зерноочисні машини» Визначення максимального розміру зерна, що пройшов через отвір решета
Розглянемо результати дослідження впливу кінематичних параметрів на можливість вільного проходження зерна через отвір без зачіпання за кромки для загального випадку просторового руху решета. Умови проходження зерен через отвори решіт, що рухаються поступально, отримані як окремі випадки.
Визначимо умови, при яких зерно кулястої форми діаметром d, що має швидкість падіння v під кутом падіння # 946; до горизонту, може пролітати без зіткнення з крайками через круглий отвір розміром l вібраційного решета, що здійснює просторові вібрації згідно із законом (4.5). Розглянемо випадки, коли центр зерна проходить через центр отвору.
Рівняння проекції траєкторії руху довільної точки решета на вертикальну площину XOZ має такий вигляд:
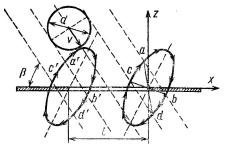
Зерно вільно пройде через отвір, якщо кромки останнього знаходяться в положенні ас або bd (рис. 8.20). Зі схеми видно, що за один період коливань решета можливі два положення кромок, що сприяють проходженню зерна через отвір, а за напівперіод - одне. Умовою проходження частинки через отвір буде нерівність
де tac - час, протягом якого кромки знаходяться в положенні, сприятливому для проходження зерна; t1 - час польоту частки.
При цьому

Рівняння проекції траєкторії руху довільної точки решета на вертикальну площину, проведену через дотичну до кола, по якій зерно рухається по решето, можна записати так:
За викладеною методикою вираз для допустимої частоти можна отримати в такому вигляді:
де # 947; - кут падіння частки у вертикальній площині, дотичній до усередненої траєкторії руху частинки (концентричного кола).
Аналіз виразів (8.72) і (8.74) показує, що вони дозволяють визначати не тільки допустимі частоти коливань, але і основні залежності між цими величинами. За умови потрапляння центру зерна в центр отвору, незалежно від частоти коливань решета, зерна розміром
також можуть пройти через отвори без взаємодії з крайками, але ця можливість залежить від частоти і амплітуди коливань решета, а також від початкової швидкості і кута падіння зерна.
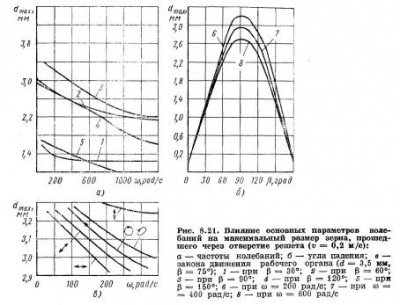
На рис. 8.21, а наведена залежність максимального розміру зерна dmax, що має можливість вільно пройти через отвір, від частоти коливань решета. Зі збільшенням частоти коливань цей розмір зменшується. Отже, можна припустити, що математичне очікування розміру проходовой фракції, за яким здійснюється поділ, зменшується.
З виразів (8.72) і (8.74) видно, що зі збільшенням швидкості падіння зерна збільшується можливість його вільного проходження через отвір. Кут падіння також істотно впливає на розмір dmax (рис. 8.21, б). Найсприятливішим для вільного проходження зерна є кут # 946; = 90 °.
Наведені формули отримані для просторового руху решета за законом (4.5), тому основні залежності між цими величинами відповідають одній будь-якій точці решета. Для інших точок ці залежності кількісно будуть відрізнятися, так як для них будуть різними R і # 949 ;.
Отримані формули придатні також для визначення залежностей між параметрами процесу при інших законах руху решіт.
1. Решето здійснює поступальні рухи по еліптичних траєкторіях у вертикальній площині із зсувом фаз коливань. Формули, отримані в даному параграфі, повністю відповідають цієї нагоди. Відмінністю буде тільки те, що в першому випадку формули придатні для однієї сукупності точок решета, у другому - для всіх його точок.
2. Решето здійснює поступальні рухи по еліптичних траєкторіях у вертикальній площині з рівними нулю зрушеннями фаз коливань. Допустима частота коливань визначається за формулою (8.72), при цьому коефіцієнти А, В і С, що входять до виразу для визначення ха і хс, приймають такий вигляд:
3. Решето здійснює поступальні коливання у вертикальній площині по кругових траєкторіях [см. формули (4.62)]. При цьому в формулу (8.72) необхідно підставити коефіцієнти А, В, С, мають такий вигляд:
4. Решето здійснює прямолінійні поступальні коливання у вертикальній площині за законом (4.66). Допустиму частоту визначаємо з виразу (8.72), а ха і хс за формулами

7. Решето робить гвинтові коливання навколо вертикальної осі за законом (4.21). Так як переміщення по дузі кола - величина пренебрежимо мала в порівнянні з радіусом цього кола, то коливання решета в кожній його точці можна розглядати як прямолінійні коливання у вертикальній площині, перпендикулярній радіусу решета, а допустиму частоту коливань визначати але формулою (8.72) з урахуванням виразів (8.77).
На рис. 8.21, в показано вплив частоти коливань на максимальний розмір пройшов через отвір решета зерна для різних законів руху робочого органу. З графіка видно, що найбільш сприятливим законом руху решета з точки зору проходження через отвір максимального зерна є коливання, близькі до вертикальних, найменш сприятливим - коливання близькі до горизонтальних.