Визначення подвійного інтеграла
Нехай на площині $ \ mathbf> $ задана обмежена замкнута область $ \ mathbf> $ з кусочно-гладкою межею, і нехай на області $ \ mathbf> $ визначена функція $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ .
Розіб'ємо область $ \ mathbf> $ довільним чином на $ \ mathbf> $ подобластей $ \ mathbf> _ $, $ \ mathbf> _ $, $ \ mathbf> _,, \ mathbf> _ $,. Символом $ \ mathbf> (\ mathbf> _) $ будемо позначати площа області $ \ mathbf> _ $; символом $ diam (\ mathbf>) $ тут і далі буде позначатися найбільша відстань між двома точками, які належать області $ \ mathbf> $: $$ diam (D) = \ mathop \ limits_ \ rho (P_1, P_2); $$ символом $ d $ позначимо найбільший з діаметрів областей $ \ mathbf> _ $: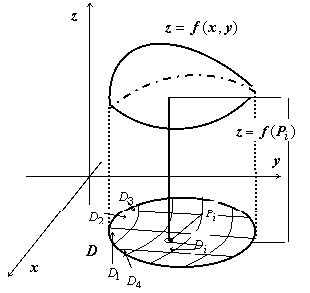
Якщо існує межа послідовності інтегральних сум при
$ D = \ mathop \ limits_ diam (D_i) \ to 0 $, що не залежить ні від способу розбиття області $ \ mathbf> $ на підобласті $ \ mathbf> _ $, ні від вибору точок $ \ mathbf> _ $, то функція $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ називається інтегрованою по області $ \ mathbf> $, а значення цієї межі називається подвійним інтегралом від функції $ \ mathbf> (\ mathbf> $, $ \ mathbf>) $ по області $ \ mathbf> $ і позначається $ \ iint \ limits_D $.Якщо розписати значення $ \ mathbf> (\ mathbf>) $ через координати точки $ \ mathbf> $, і уявити $ \ mathbf> $ як $ \ mathbf> = \ mathbf> $, отримаємо інше позначення подвійного інтеграла: $ \ iint \ limits_D $. Отже, коротко,Теорема існування подвійного інтеграла
Якщо підінтегральна функція $ \ mathbf> (\ mathbf>, \ mathbf>) $ неперервна на області $ \ mathbf> $, то вона інтегровна по цій області.
Геометричний сенс подвійного інтеграла. Геометричний сенс кожного доданка інтегральної суми
З геометричної точки зору інтегральна сума являє собою суму обсягів циліндрів з підставами $ s (D _) $ і висотами $ f (P_i) $.
Якщо $ f (x, y) \ geqslant 0 $, то $ f (P_i) \ cdot s (D_i) $ - обсяг прямого циліндра з основою $ \ mathbf> _ $ висоти $ \ mathbf> (\ mathbf> _) $ ; вся інтегральна сума $ \ sum \ limits_ ^ n $ - сума обсягів таких циліндрів, тобто обсяг деякого ступеневої тіла - висота сходинки, розташованої над підобластю $ \ mathbf> _ $, дорівнює $ \ mathbf> (\ mathbf> _) $. Коли $ d = \ mathop \ limits_ diam (D_i) \ to 0 $, це поетапне тіло стає все ближче до зображеного на малюнку тілу, обмеженому знизу областю $ \ mathbf> $, зверху - поверхнею $ \ mathbf> = \ mathbf> ( \ mathbf> $, $ \ mathbf>) $, з циліндричною бічною поверхнею, що направляє якої є межа області $ \ mathbf> $, а утворюють паралельні осі $ \ mathbf> $. Подвійний інтеграл $ \ iint \ limits_D $ дорівнює обсягу цього тіла.Читайте також:
Поверхневий інтеграл першого роду і його властивості
Механічні додатки криволінійного інтеграла 1-го роду
Інваріантне визначення дивергенції
Механічні додатки потрійного інтеграла
Перейти до змісту $ \ Rightarrow \ Rightarrow \ Rightarrow $