Видавничий дім Далекосхідного федерального університету
Мета даної роботи - вивчити закони коливань математичного маятника і ознайомитися з методикою експериментального визначення прискорення вільного падіння з його допомогою.
Коротка теорія. Механічний рух тіл - зміна їх положення в просторі з плином часу. Рух тіла поділяється на три види:
поступальний - всі крапки тіла рухаються однаково (швидкість і прискорення всіх точок тіла однакові і за величиною і за напрямком);
обертальний - всі крапки тіла рухаються по колах навколо загального центру або осі;
коливальний - всі крапки тіла здійснюють зворотно-поступальний або зворотно-обертальний рух. При лінійному коливальному русі точка М не виходить за межі будь-якого отрезкаKLна цієї лінії і багаторазово проходить через одні й ті самі положення всередині цього відрізка (Рис.1). Коливальний рух характеризується певною повторюваністю в часі. Якщо при такому русі існує певний проміжок часу Т, через який рух точки М в точності повторюється, то таке коливання називаетсяперіодіческім.
Існує безліч різних видів періодичних коливань, найпростішими з яких є гармонійні коливання - коливання, при яких фізична (або будь-яка інша) величина змінюється з часом за синусоїдальним або косинусоидальной закону. Гармонійні коливання - це ідеалізація, що займає серед всіх інших коливань особливе місце, що зумовлено двома причинами:
1) коливання, що зустрічаються в природі і техніці, часто мають характер, близький до гармонійних коливань;
2) будь-негармоніческое коливання можна представити у вигляді суми (накладень) різних гармонійних коливань.
Кинематическое рівняння гармонійних коливань має вигляд
У рівняннях (1) і (2):
Х -смещеніе (відхилення) хитається точки від положення рівноваги в момент часу t;
А -амплітуда коливань, це величина, яка визначає максимальне відхилення коливної точки від положення рівноваги (А = | Хmax |). Амплітуда і зміщення в системі СІ вимірюються в метрах.
ω -циклічна частота, величина, що показує число повних коливань, що відбуваються в теченіе2π секунд. В системі СІ циклічна частота вимірюється в с -1. Циклічна частота пов'язана з періодом колебанійТ і частотойν.
Т-період коливань. величина, яка визначає час одного повного коливання (проміжок часу між двома послідовними проходженнями коливається точки через одне і те ж положення в одному і тому ж напрямку) .Т =. іліω =. Період в системі СІ вимірюється в секундах.
ν-частота коливань, величина, що показує число повних коливань за одиницю часу. Частота пов'язана з періодом і циклічною частотою співвідношеннями: ν =. В системі СІ частота ν вимірюється в герцах (герц- одне коливання за секунду).
ωt + φо фаза коливань, величина, яка визначає величину зсуву хитається точки від положення рівноваги в даний момент часу t.
φо - початкова фаза. величина, яка визначає величину зсуву Х хитається точки від положення рівноваги в початковий момент часу (t = 0). Початкова фаза і фаза коливань вимірюються в кутових одиницях, тобто в градусах або в радіанах (в частках π).
Використовуючи одне з кінематичних рівнянь гармонійних коливань, наприклад рівняння (1), знайдемо кінематичні характеристики цих коливань - швидкість і прискорення.
Швидкість V - це перша похідна за часом від зсуву Х:
V = = AωCos (ωt + φо), (3)
де величина Aω - амплітуда швидкості Аv гармонійних коливань.
Прискорення гармонійних коливань α визначиться як перша похідна за часом від швидкості гармонійних коливань, або друга похідна за часом від зсуву
α = == - Аω2Sin (ωt + φо), (4)
де величина А ω2 - амплітуда прискорення Аα. З урахуванням рівняння (1), прискорення гармонійних коливань (рівняння (4)) можна уявити в іншому вигляді:
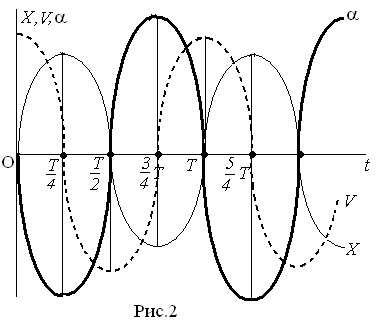
З формул (1), (2) і (3) видно, що при гармонічних коливаннях зміщення, швидкість і прискорення характеризуються однаковою циклічною частотою і, отже періодом (Т =). Фази коливань зазначених величин різні: коливання швидкості випереджає коливання зсуву по фазі на (за часом на), коливання прискорення випереджає коливання зсуву по фазі на π, (за часом на).
На малюнку 2 представлені графіки залежності від часу зміщення, швидкості і прискорення (початкова фаза φо = 0). Як видно з малюнка, в момент проходження хитається точкою положення рівноваги (Х = 0) її швидкість максимальна. Коли ж точка максимально відхилиться від положення рівноваги (Х = + А іліХ = -А), її швидкість дорівнює нулю, а прискорення стає максимальним. При цьому, знак прискорення завжди протилежний знаку зсуву, тобто прискорення завжди спрямоване до положення рівноваги хитається точки.
Знаючи масу mколеблющейся частки (матеріальна точка) і її прискорення, яке визначається рівнянням (5), знайдемо силу, під дією якої відбуваються гармонійні колеба- ня. Згідно з другим законом Ньютона ця сила дорівнює
де k = mω2 - коефіцієнт пропорційності є постійною величиною для даного осцилятора (осцилятор - фізична система, яка здійснює коливання). З рівняння (6) видно, що сила, що викликає гармонійнеколивання, пропорційна смещеніюХ і спрямована проти зсуву, на що вказує знак мінус. Ця сила прагне повернути коливається точку в положення рівноваги, тому її називаютвозвращающей силою. Такою силою, наприклад, може битьсіла пружності. що виникає при малих деформаціях будь-якого виду, яка, відповідно до закону Гука, пропорційна деформації (зміщення) ΔХ і протилежна йому за знаком. Ті, що повертають сили можуть мати і іншу, що не пружну природу. У цих випадках вони називаютсяквазіупругімі силами (тобто «як би подібні пружним силам»). Коеффіціентk. визначає значення сили, що викликає зсув, називають коефіцієнтом повертає сили. Як сили пружності, так і квазіпружної сили є внутрішніми силами хитається системи. Следовательно.гармоніческіе коливання відбуваються під дією внутрішніх пружних, або на них схожих, квазіупругіх сил. Коливання, що відбуваються тільки під дією внутрішніх сил, називаютсясвободнимі (або власними).
Енергія гармонічних коливань. Для гармонійних коливань виконується закон збереження механічної енергії, згідно якого повна енергія Е гармонійного осцилятора залишається постійною. Доведемо це твердження. Повна механічна енергіяЕ складається з кінетіческойEk і потенціальнойEp енергій
Кінетична енергія є мірою руху і для матеріальної точки (або поступального руху твердого тіла) визначається за формулою
де m - маса коливається точки, V - швидкість її руху.
Потенційна енергія визначається станом тіла або його положенням в просторі. Для пружних (або квазіупругіх) сил потенційна енергія тіла визначається за формулою
де k - коефіцієнт пружності, Х - зміщення коливної точки від положення рівноваги.
вираз для повної механічної енергії гармонійних коливань:
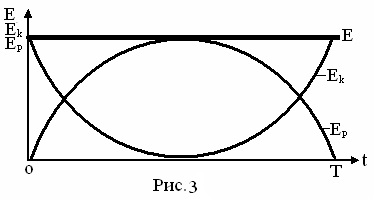
Величини, що стоять в рівнянні справа (kи А) - постійні для даного гармонійного осцилятора і, отже, повна енергія гармонічних колебанійЕ для даного осцилятора є величина постійна. При цьому, як кінетична, так і потенційна енергії, змінюються в протифазі, відповідно, по квадратичним законам косинуса і синуса (рис. 3).
Математичний маятник, період його коливань. Прикладом механічних гармонійних коливань під дією квазіупругіх сил є коливання математичного маятника. Математичним маятником називають ідеалізовану систему, що складається з невагомою і нерастяжимой нитки, на якій підвішена маса, зосереджена в одній точці. Досить хорошим наближенням до математичного маятника служить невеликий важкий кулька, підвішений на довгій тонкій нерастяжимой нитки (рис.4). На кульку маятника завжди діють дві сили: сила тяжіння сила натягу нитки. У положенні рівноваги (вільно висить маятник) сума зазначених сил дорівнює нулю. На кульку маятника, відхиленого від положення рівноваги на уголφ. буде діяти повертає сила, рівна результуючої двох сил: сили тяжіння (g-прискорення вільного падіння) і сили натягу нитки.
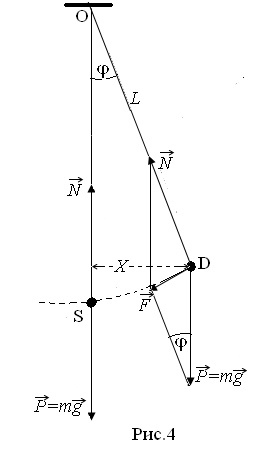
Під дією цієї повертає сили, маятник почне прискорено рухатися від точкіD до точки S (положенню рівноваги). У точці S величина сили дорівнює нулю, але так як маятник має масу m і до моменту проходження точки S має швидкість V. то він за інерцією пройде цю точку. При подальшому русі маятника по дузі його швидкість буде знижуватися внаслідок того, що напрямок сили зміниться і буде протилежно напрямку руху маятника. У кінцевій точці руху маятник зупиниться і відразу ж почне рух до точки S. Таким чином, маятник буде здійснювати під дією сили коливальні рухи. Якщо на маятник не діють сили тертя, то він буде робити коливальні рухи нескінченно довго. З малюнка 4 видно, що величина сілисвязана з величиною сили тяжіння, співвідношенням:
Залежність повертає сили від зсуву, що характеризується кутом φ, в рівнянні (11), нелінійна, отже, і коливання маятника будуть не гармонійними. Однак, в разі малих коливань маятника, коли кут відхилення φ настільки малий (до 5 о), чтоSinφ = ≈ φ. повертає сила пропорційна куту φ і в цьому випадку (при малих відхиленнях) можна вважати, що коливання маятника відбуваються під дією квазіпружної сили, і отже, коливання є гармонійними. Малим кутах отклоненіяφ відповідає і мала величина зсуву. Підставивши в рівняння (11) вместоSin. велічінуі, враховуючи, що при малих кутах отклоненіяφ. вектор сілипрактіческі співпаде з відрізком зміщення Х, але спрямований протилежно відхиленню, остаточно можна записати повертає (квазіпружної) силу у вигляді
Отже, при малих кутах відхилення φ. на маятник буде діяти квазіупругая сила і він буде здійснювати гармонічні коливання. Знайдемо період таких гармонійних коливань математичного маятника. Для цього запишемо другий закон Ньютона в скалярному вигляді:
де α = - прискорення коливається кульки математичного маятника, Скоротивши в рівнянні (13) масу, отримаємо рівняння у вигляді: = - або
Так як в цих рівняннях величини g іLвсегда позитивні, то їхнє ставлення можна прирівняти до квадрату деякої величини ω 2: