Скористаємося рівнянням (4) і візьмемо від нього похідну за часом
В (8) при одиничних вектори стоять проекції вектора швидкості на координатні осі
Проекції швидкості на координатні осі визначаються як перші похідні за часом від відповідних координат.
Знаючи проекції, можна знайти модуль вектора і його напрямок
Визначення швидкості при природному способі
Нехай дана траєкторія матеріальної точки і закон зміни криволінійної координати. Припустимо, при t1 точка мав
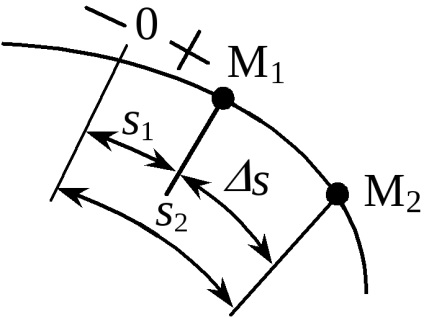
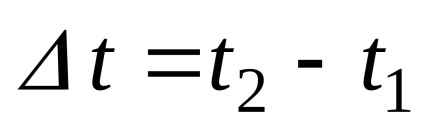
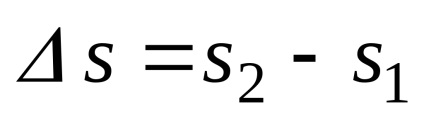
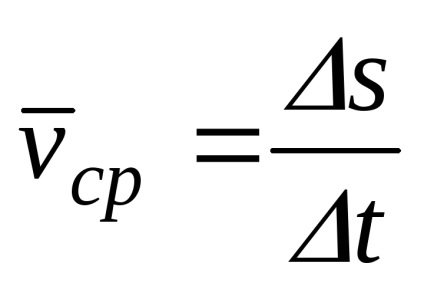
Для знаходження швидкості в заданий момент часу перейдемо до межі
,
Вектор швидкості точки при природному способі завдання руху визначається як перша похідна за часом від криволінійної координати.
Під прискоренням матеріальної точки розуміють векторну величину, що характеризує швидкість зміни вектора швидкості точки за величиною і напрямком з плином часу.
Прискорення точки при векторному способі завдання руху
Розглянемо точку в два моменти часу t1 (
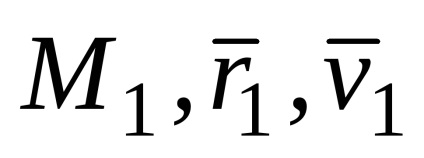
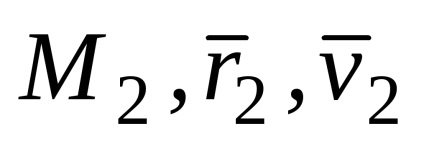
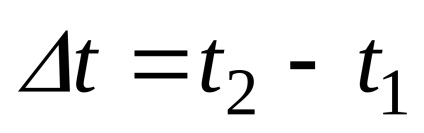
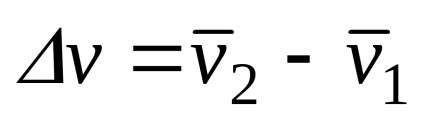
вектор

П
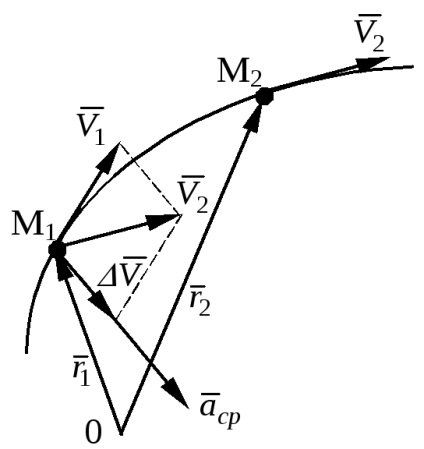
Для знаходження прискорення в заданий момент часу перейдемо до межі
,
Прискорення точки в даний момент часу визначається як друга похідна за часом від радіус-вектора точки або перша похідна від вектора швидкості за часом.
Вектор прискорення розташований в дотичної площині і спрямований в бік угнутості траєкторії.
Прискорення точки при координатному способі завдання руху
Скористаємося рівнянням зв'язку векторного і координатного способів завдання руху
.
І візьмемо від нього другу похідну
,
У рівнянні (15) при одиничних вектори стоять проекції вектора прискорення на координатні осі
Проекції прискорення на координатні осі визначаються як перші похідні за часом від проекцій швидкості або як другі похідні від відповідних координат за часом.
Модуль і напрям вектора прискорення можна знайти за такими виразами
Прискорення точки при природному способі завдання руху
П
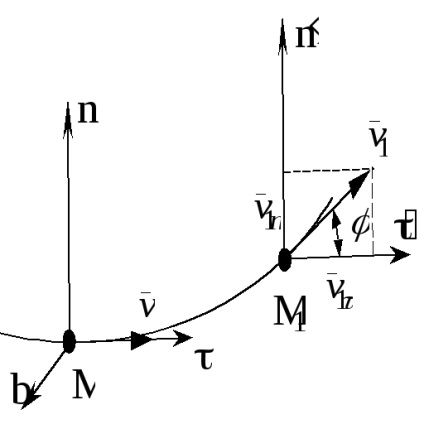
Прискорення при цьому визначається через його проекції на осі природної системи координат, що рухається разом з точкою M. Осі при цьому спрямовані наступним чином:
M - дотична, спрямована уздовж дотичній до траєкторії, в сторону позитивного відліку відстані,
Mn - головна нормаль, спрямована по нормалі, що лежить в дотичній площині, і спрямована в бік угнутості траєкторії,
Mb - бінормаль, перпендикулярна площині Mn і утворює з першими осями праву трійку.
Так як вектор прискорення лежить в дотичній площині, то ab = 0. Знайдемо проекції прискорення на інші осі.
Спроектуємо (19) на координатні осі
Проведемо через точку M1 осі паралельні осях в точці M і знайдемо проекції швидкості:
де - так званий кут суміжності.
Підставляємо (22) в (20)

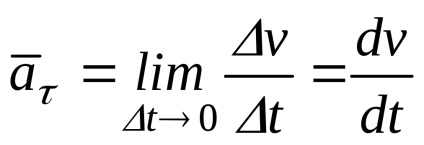
Дотичне прискорення точки визначається першої похідної за часом від швидкості або другій похідній за часом від криволінійної координати.
Дотичне прискорення характеризує зміну вектора швидкості за величиною.
Підставами (22) в (21)
.
Помножимо чисельник і знаменник на s щоб отримати відомі межі
де
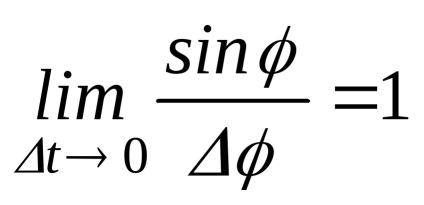
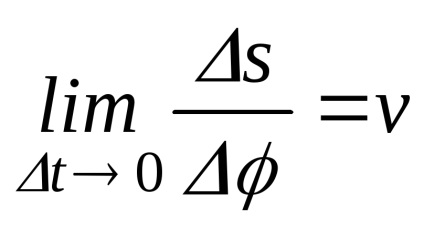
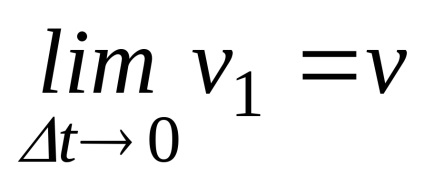
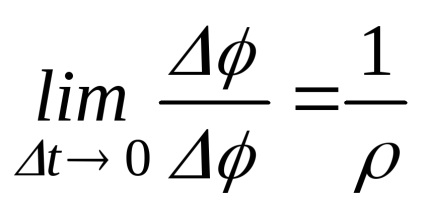
Підставляючи обчислені межі в (24), отримаємо
Нормальне прискорення точки визначається відношенням квадрата швидкості до радіуса кривизни траєкторії в даній точці.
Нормальне прискорення характеризує зміну вектора швидкості у напрямку і завжди направлено в сторону угнутості траєкторії.
Остаточно отримаємо проекції прискорення матеріальної точки на осі природної системи координат і модуль вектора