1. Закон всесвітнього тяжіння
Ви вже знаєте, що між усіма тілами діють сили тяжіння, звані силами всесвітнього тяжіння.
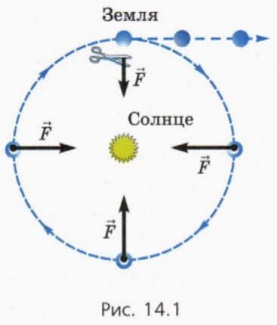
Їх дія проявляється, наприклад, в тому, що тіла падають на Землю, Місяць обертається навколо Землі, а планети обертаються навколо Сонця. Якби сили тяжіння зникли, Земля полетіла б від Сонця (рис. 14.1).
Закон всесвітнього тяжіння сформулював у другій половині 17-го століття Ісаак Ньютон.
Дві матеріальні точки масою m1 і m2 знаходяться на відстані R, притягуються з силами, прямо пропорційними добутку їх мас і обернено пропорційними квадрату відстані між ними. Модуль кожної сили
Коефіцієнт пропорційності G називають гравітаційною сталою. (Від латинського «гравітас» - тяжкість.) Вимірювання показали, що
G = 6,67 * 10 -11 Н * м 2 / кг 2. (2)
Закон всесвітнього тяжіння розкриває ще одну важливу властивість маси тіла: вона є мірою не тільки інертності тіла, але і його гравітаційних властивостей.
1. Чому рівні сили тяжіння двох матеріальних точок масою 1 кг кожна, що знаходяться на відстані 1 м один від одного? У скільки разів ця сила більше або менше ваги комара, маса якого 2,5 мг?
Така мала значення гравітаційної постійної пояснює, чому ми не помічаємо гравітаційного тяжіння між людьми, які нас предметами.
2. Оцініть сили гравітаційного тяжіння двох людей, що знаходяться на відстані 10 м один від одного.
Сили тяжіння помітно виявляють себе тільки тоді, коли хоча б одне з взаємодіючих тіл має величезну масу - наприклад, є зіркою або планетою.
3. Як зміниться сила тяжіння між двома матеріальними точками, якщо відстань між ними збільшити в 3 рази?
4. Дві матеріальні точки масою m кожна притягуються з силою F. З якою силою притягуються матеріальні точки масою 2m і Зm, що знаходяться на такій же відстані?
2. Рух планет навколо Сонця
Відстань від Сонця до будь-якої планети у багато разів більше розмірів Сонця і планети. Тому при розгляді руху планет їх можна вважати матеріальними точками. Отже, сила тяжіння планети до Сонця
де m - маса планети, MС - маса Сонця, R - відстань від Сонця до планети.
Будемо вважати, що планета рухається навколо Сонця рівномірно по колу. Тоді швидкість руху планети можна знайти, якщо врахувати, що прискорення планети a = v 2 / R обумовлено дією сили F тяжіння Сонця і тим, що згідно з другим законом Ньютона F = ma.
5. Доведіть, що швидкість планети
З цієї формули випливає, що чим більше радіус орбіти, тим менше швидкість планети.
6. Радіус орбіти Сатурна приблизно в 9 разів більше радіуса орбіти Землі. Знайдіть усно, чому приблизно дорівнює швидкість Сатурна, якщо Земля рухається по своїй орбіті зі швидкістю 30 км / с?
За час, що дорівнює одному періоду обертання T, планета, рухаючись зі швидкістю v, проходить шлях, рівний довжині кола радіуса R.
7. Доведіть, що період обертання планети
З цієї формули випливає, що чим більше радіус орбіти, тим більше період обертання планети.
8. Оцініть період обертання Сатурна (в земних роках).
9. Доведіть, що для всіх планет Сонячної системи
Підказка. Скористайтеся формулою (5).
З формули (6) випливає, що для всіх планет Сонячної системи відношення куба радіуса орбіти до квадрату періоду звернення однаково. Цю закономірність (її називають третім законом Кеплера) виявив німецький вчений Йоганн Кеплер на підставі результатів багаторічних спостережень датського астронома Тихо Браге.
3. Умови застосовності формули для закону всесвітнього тяжіння
Ньютон довів, що формулу
для сили тяжіння двох матеріальних точок можна застосовувати також:
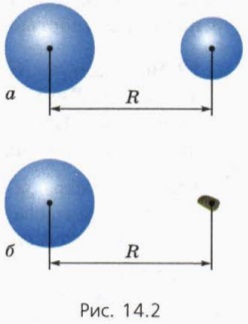
- для однорідних куль і сфер (R - відстань між центрами куль або сфер, рис. 14.2, а);
- для однорідної кулі (сфери) і матеріальної точки (R - відстань від центру кулі (сфери) до матеріальної точки, рис. 14.2, б).
4. Сила тяжіння і закон всесвітнього тяжіння
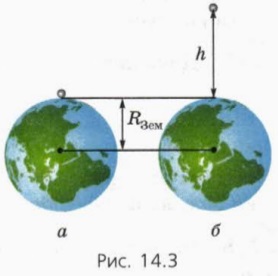
Друге з наведених вище умов означає, що за формулою (1) можна знайти силу тяжіння тіла будь-якої форми до однорідного кулі, який набагато більше цього тіла. Тому за формулою (1) можна розрахувати силу тяжіння до Землі тіла, що знаходиться на її поверхні (рис. 14.3, а). Ми отримаємо вираз для сили тяжіння:
(Земля не є однорідним шаром, але її можна вважати сферически симетричною. Цього достатньо для можливості застосування формули (1).)
10. Доведіть, що поблизу поверхні Землі
де MЗем - маса Землі, RЗем - її радіус.
Підказка. Використовуйте формулу (7) і те, що Fт = mg.
Користуючись формулою (1), можна знайти прискорення вільного падіння на висоті h над поверхнею Землі (рис. 14.3, б).
11. Доведіть, що
12. Чому дорівнює прискорення вільного падіння на висоті над поверхнею Землі, рівної її радіусу?
13. У скільки разів прискорення вільного падіння на поверхні Місяця менше, ніж на поверхні Землі?
Підказка. Скористайтеся формулою (8), в якій масу і радіус Землі замініть на масу і радіус Місяця.
14. Радіус зірки білий карлик може бути дорівнює радіусу Землі, а її маса - рівній масі Сонця. Чому дорівнює вага кілограмової гирі на поверхні такого «карлика»?
5. Перша космічна швидкість
Уявімо собі, що на дуже високій горі встановили величезну гармату і стріляють з неї в горизонтальному напрямку (рис. 14.4).
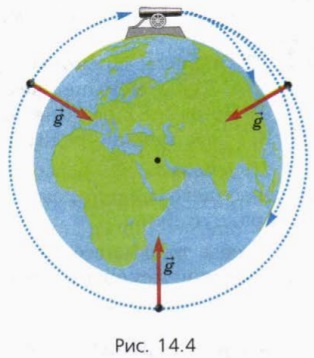
Чим більше початкова швидкість снаряда, тим далі він впаде. Він не впаде взагалі, якщо підібрати його початкову швидкість так, щоб він рухався навколо Землі по колу. Летячи по круговій орбіті, снаряд стане тоді штучним супутником Землі.
Нехай наш снаряд-супутник рухається по низькій навколоземній орбіті (так називають орбіту, радіус якої можна прийняти рівним радіусу Землі RЗем).
При рівномірному русі по колу супутник рухається з доцентровим прискоренням a = v2 / RЗем, де v - швидкість супутника. Це прискорення зумовлено дією сили тяжіння. Отже, супутник рухається з прискоренням вільного падіння, спрямованим до центру Землі (рис. 14.4). Тому a = g.
15. Доведіть, що при русі по низькій навколоземній орбіті швидкість супутника
Підказка. Скористайтеся формулою a = v 2 / r для центростремительного прискорення і тим, що при русі по орбіті радіуса RЗем прискорення супутника дорівнює прискоренню вільного падіння.
Швидкість v1. яку необхідно повідомити тілу, щоб воно рухалося під дією сили тяжіння по круговій орбіті поблизу поверхні Землі, називають першою космічною швидкістю. Вона приблизно дорівнює 8 км / с.
16. Виразіть першу космічну швидкість через гравітаційну постійну, масу і радіус Землі.
17. Оцініть, у скільки разів перша космічна швидкість для Місяця менше, ніж для Землі. Прийміть, що маса Місяця в 81 разів менше маси Землі, а радіус Місяця в 3,7 рази менше радіуса Землі.
Підказка. У формулі, отриманої при виконанні попереднього завдання, замініть масу і радіус Землі на масу і радіус Місяця.
Щоб тіло назавжди залишило околиці Землі, йому треба повідомити швидкість, рівну приблизно 11,2 км / с. Її називають другою космічною швидкістю.
6. Як виміряли гравітаційну постійну
Якщо вважати відомими прискорення вільного падіння g поблизу поверхні Землі, масу і радіус Землі, то значення гравітаційної постійної G можна легко визначити за допомогою формули (7). Проблема, однак, у тому, що до кінця 18-го століття масу Землі виміряти не вдавалося.
Тому, щоб знайти значення гравітаційної постійної G, треба було виміряти силу тяжіння двох тіл відомої маси, що знаходяться на певній відстані один від одного. В кінці 18-го століття такий досвід зміг поставити англійський вчений Генрі Кавендіш.
Він підвісив на тонкої пружної нитки легкий горизонтальний стрижень з невеликими металевими кульками a і b і по куту повороту нитки виміряв сили тяжіння, що діють на ці кулі з боку великих металевих куль А і В (рис. 14.5). Малі кути повороту нитки вчений вимірював зі зміщення «зайчика» від прикріпленого до нитки дзеркальця.
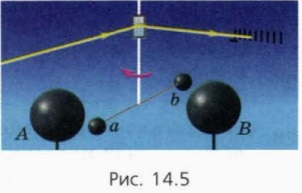
Цей досвід Кавендіша образно назвали «зважуванням Землі», тому що цей досвід вперше дозволив виміряти масу Землі.
18. Виразіть масу Землі через G, g і RЗем.
Додаткові питання і завдання
19. Два корабля масою 6000 т кожен притягуються з силами по 2 мН. Яке відстань між кораблями?
20. З якою силою Сонце притягує Землю?
21. З якою силою людина масою 60 кг притягує Сонце?
22. Чому дорівнює прискорення вільного падіння на відстані від поверхні Землі, що дорівнює її діаметру?
23. У скільки разів прискорення Місяця, обумовлене тяжінням Землі, менше прискорення вільного падіння на поверхні Землі?
24. Прискорення вільного падіння на поверхні Марса в 2,65 разів менше прискорення вільного падіння на поверхні Землі. Радіус Марса приблизно дорівнює 3400 км. У скільки разів маса Марса менше маси Землі?
25. Чому дорівнює період обертання штучного супутника Землі на низькій навколоземній орбіті?
26. Чому дорівнює перша космічна швидкість для Марса? Маса Марса 6,4 * 10 23 кг, а радіус 3400 км.