Розгляд фулеренів і нанотрубок неможливо, якщо не розібратися в природі цих явищ. Для початку розглянемо склад фулеренів і нанотрубок.
Вуглець - хімічний елемент, символ С, атомний номер 6, атомна маса 12.011. Звичайними формами існування вуглецю у вільному стані є алмаз і графіт, зустрічаються в природі. Основними відмінностями в будові алмазу і графіту - кристалічна решітка.
Алмаз. Структура кристалічної решітки показана на рис. 1.
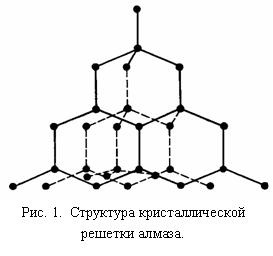
Елементарна комірка кристала алмаза являє собою тетраедр, в центрі і чотирьох вершинах якого розташовані атоми вуглецю. Атоми, розташовані в вершинах тетраедра, утворюють центр нового тетраедра і, таким чином, також оточені кожний ще чотирма атомами і т.д. Координаційне число вуглецю в решітці алмазу, отже, дорівнює чотирьом. Всі атоми вуглецю в кристалічній решітці розташовані на однаковій відстані (154 пм) один від одного. Кожен з них пов'язаний з іншими неполярной ковалентним зв'язком і утворює в кристалі, яких би розмірів він не був, одну гігантську молекулу.
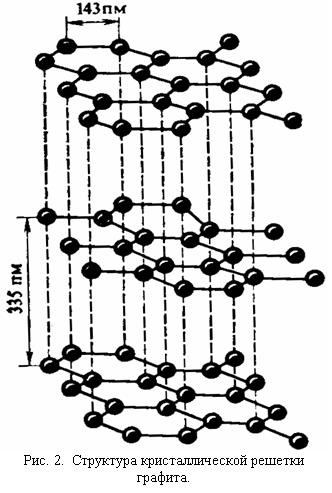
Графіт. Структура кристалічної решітки графіту показана на рис. 2. Кристали графіту побудовані з паралельних один одному площин, в яких розташовані атоми вуглецю по кутах правильних шестикутників. Відстань між сусідніми атомами вуглецю (сторона кожного шестикутника) 143 пм, між сусідніми площинами 335 пм. Кожна проміжна площину кілька зміщена по відношенню до сусідніх площинах, як це видно на малюнку. Кожен атом вуглецю пов'язаний з трьома сусідніми в площинах атомами неполярних ковалентними зв'язками. Кожен атом вуглецю в атомній решітці графіту пов'язаний з трьома сусідніми атомами вуглецю, трьома sp 2 -sp 2 загальними електронними парами, розташованими відповідно до sp 2 - гібридизацією, під кутами в 120 град, т. Е. Кожні чотири пов'язаних між собою атома вуглецю в графіті розташовані в центрі і вершинах рівностороннього трикутника. Четверті валентні електрони кожного атома розташовуються між площинами і ведуть себе подібно електронам металу, чим і пояснюється електрична провідність графіту в напрямку площин. Зв'язок між атомами вуглецю, розташованими в сусідніх площинах, дуже слабка (межмолекулярная, або ван-дер-ваальсова), хоча почасти, завдяки присутності електронів провідності, схожа на металеву. У зв'язку з такими особливостями кристали графіту легко розшаровуються на окремі лусочки навіть при малих навантаженнях.
Унікальна здатність атомів вуглецю з'єднуватися між собою з утворенням міцних і довгих ланцюгів і циклів призвела до виникнення величезного числа різноманітних з'єднань-ний вуглецю, що вивчаються органічною хімією.
Теплопровідність графіту, виміряна в напрямку площині шарів, в п'ять разів більше теплопровідності, изме-ренной в поперечному напрямку; електричні-кая провідність в площинному напрямку в десять тисяч разів перевищує провідність в поперечному напрямку.
Електронна конфі-гурація атома вуглецю така: 1s 2 2s 2 2p 2. Отже, його чотири зовнішніх електрона не однакові - вони відповідають різним орбиталям; два електрони не спарені. У зв'язаному стані (валентном) один з електронів 2s переходить на р-орбіталь (для цього знадобиться близько 96 ккал / моль) так, що стан атома може бути виражено: 1s 2 2s 2p 3. В результаті ми отримаємо атом з трьома 2р і одним 2s-електроном: 2s2px2py2pz.
Можливі кілька видів гібридизації: sp, sp 2 та sp 3
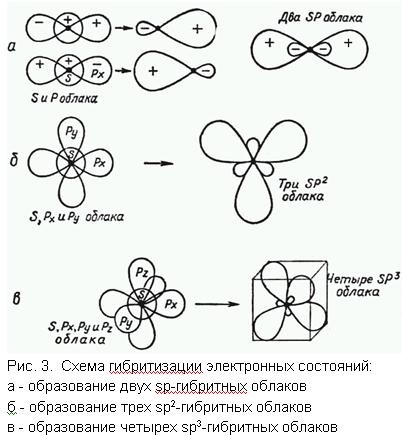
При гібридизації типу sp змішуються атомні орбіталі s і р. При цьому орбіталі, наприклад, рy і рz не змінюються, а орбіталі рx і s дають гібридну форму. Так як гібридна функція може мати вигляд s + p або s-р, то виходять дві орбіталі, направ-лені диамет-рально протипожежні-помилково один одному (рис. 3а).
Якщо відбувається із-дит гібридизація s і двох р-функцій, наприклад рx і ру (рz залишається незмінною), то виходять три Тригональна атом-ні орбіталі типу sp 2. Ці орбіталі на схемі мають вигляд конюшини (рис. 3б). Цей вид гібридних орбіта-лей виявився дуже важливим для опису подвійних зв'язків.
При гібридизації типу sp 3 змішуються всі атомні орбіталі s і р. При цьому всі орбіталі дають гібридну форму. Гібридні орбіталі мають чітку спрямованість: орбіталі атома вуглецю направлені до кутів тетраедра, в центрі якого міститься атом вуглецю. Схематично посилення спрямованості - орієнтація електронної хмари - показано на малюнку 3в. Очевидно, що це є наслідок ослаблення частин атомних орбіталей, мають різні знаки, і посилення частин атомних орбіталей, що мають однакові знаки.
Отримання нанотрубок. Найбільш широко поширений метод одержання вуглецевих нанотрубок використовує термічне розпорошення графітового електрода в плазмі дугового розряду, що горить в атмосфері He. Цей метод, що лежить також в основі найбільш ефективної технології виробництва фулеренів, дозволяє отримати нанотрубки в кількості, достатній для детального дослідження їх фізико-механічних властивостей. У дугового розряду постійного струму з графітовими електродами при напрузі 15 - 20 В, струмі в декілька десятків ампер, межелектродном відстані в кілька міліметрів і тиску He у кілька сот торр відбувається інтенсивне термічне розпорошення матеріалу анода. Продукти розпилення містять, поряд з частинками графіту, також деяку кількість фулеренів, осідають на охолоджених стінках розрядної камери, а також на поверхні катода, більш холодного в порівнянні з анодом. Розглядаючи цей катодний осад за допомогою електронного мікроскопа виявили, що в ньому містяться протяжні циліндричні трубки довжиною понад мікрона і діаметром в декілька нанометрів, поверхня яких освічена графітовими шарами. Трубки мають куполоподібні наконечники, що містять, подібно до молекул фулеренів, шести- і п'ятикутник.
Як зазначалося вище, структурно графіт, з якого їх одержують, складається тільки з шестикутників. Розглянемо тепер питання, звідки в складі даних наноструктур з'являються п'ятикутник. Для цього необхідно звернутися до однієї з теорем топології, яка дає відповідь на питання: якими фігурами можна «покрити» сферу, запаяну і не запаяну трубки. Далі наведемо доказ даної теореми і деякі її наслідки.
Нехай на сфері (або Гомеоморфний їй поверхні) накреслена зв'язний граф G, що має В вершин і Р ребер і розбиває сферу на Г областей (граней); тоді справедливо рівність В-Р + Г = 2 (1). Це теорема Ейлера.
Перед доказом цієї теореми варто пригадати деякі визначення.
Кінцевим графом G називається фігура, що складається з кінцевого числа дуг. У ньому є кінцеве число вершин, і деякі з цих точок з'єднуються непересічними дугами (ребрами графа). Зв'язковим графом називається граф, будь-які дві вершини якого можна з'єднати кривої, що проходить по ребрах графа.
Контуром в графі називається замкнута ланцюжок ребер, об'єднання яких є лінією, гомеоморфними окружності.
Деревом називається зв'язний граф, що не містить жодного контура.
Індекс точки називається число дуг, що сходяться в даній точці.
Також слід довести наступну теорему:
Для будь-якого дерева, що має У вершин і Р ребер, справедливо співвідношення
Для доказу проведемо індукцію по числу ребер Р. При Р = 1 (дерево має одне ребро і дві вершини) співвідношення (2) справедливо. Припустимо, що для будь-якого дерева, що має n ребер, співвідношення (2) вже доведено, і нехай G - дерево, що має n + 1 ребро. Так як граф G зв'язний, то його можна отримати з деякого зв'язного графа G` додаванням одного ребра r.
Дійсно, будь-який зв'язний граф може бути отриманий таким чином: ми беремо одне ребро, потім приєднуємо до нього ще одне ребро так, щоб знову вийшов зв'язний граф, потім приєднуємо ще одне ребро (так, щоб знову вийшов зв'язний граф) і т.д. Це можливо, якщо вдасться його викреслити «одним розчерком». А це, в свою чергу, можливо, якщо дозволити «проходити» кожне ребро рівно два рази.