Розкладання в тригонометричний ряд Фур'є за допомогою Вольфрам Альфа
На практиці, зокрема для студентів вузів або для технічних додатків, частіше виникає необхідність швидко знайти розкладання функції саме в вигляді тригонометричного ряду Фур'є. Тому деякі читачі запитують: як змусити Вольфрам Альфа вивести розкладання заданої функції в ряд Фур'є в верхній частині сторінки, безпосередньо відразу під полем запиту.
Відповідь на це я знайшов логічним шляхом.
Оскільки тригонометричну форму ряду Фур'є система Вольфрам Альфа вважає альтернативної, це означає, що спочатку вона обчислює коефіцієнти експоненціального ряду, а вже потім перетворює їх (спрощує, призводить до тригонометричної формі) за допомогою формули Ейлера (Euler formula).
Природно, щоб в першу чергу отримати розкладання функції в тригонометричний ряд Фур'є, потрібно відразу ж поставити системі саме це завдання, а саме: спростити розкладання функції в ряд Фур'є, що легко робиться за допомогою ключового слова simplify.
Таким чином, щоб отримати розкладання функції в тригонометричний ряд Фур'є за допомогою Вольфрам Альфа, слід використовувати запит виду:
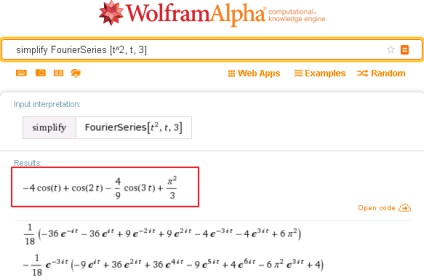
Як видно на малюнку, тут система спочатку виводить 3 перших члена розкладання функції t ^ 2 в тригонометричний ряд Фур'є, і вже в другу чергу показує відповідний ряд Фур'є в експоненційної формі.
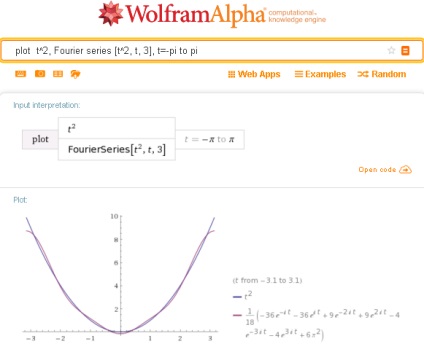
До речі, якщо раптом вас зацікавить наскільки точно ряд Фур'є аппроксимирует цю функцію, це можна побачити і досить просто. Досить порівняти два графіка в одній системі координат - графік даної функції з її тригонометричної аппроксимацией, вказавши їх через кому: