67. У будь-яких умовах стрільби закономірність розсіювання залишається незмінною, але величина площі розсіювання змінюється в залежності від вишколу стріляючого, виду зброї, боєприпасів, прицільних пристосувань, положення для стрільби, дальності стрільби, метеорологічних та інших умов стрільби.
Для вимірювання величини площі розсіювання, порівняння розсіювання куль (гранат) різних видів зброї, а також для оцінки розсіювання куль (гранат) одного і того ж зброї при різних умовах стрільби можуть застосовуватися такі заходи (одиниці вимірювання) розсіювання: серединне відхилення, серцевинна смуга і радіус кола, що вміщає кращу половину влучень або все попадання.
68. Серединний відхиленням називається таке відхилення, яке в ряді всіх відхилень, виписаних по абсолютній величині в зростаючому або спадному порядку, займає середнє місце.
Серединне відхилення є основним заходом розсіювання. Воно зазвичай позначається: Вд - серединне відхилення по дальності; Bв - серединне відхилення по висоті; Вб - серединне відхилення по бічному напрямку.
Для визначення величини серединного відхилення по одному з напрямків необхідно виписати всі відхилення в ряд в зростаючому або спадному порядку по абсолютній величині. Відхилення, що стоїть посередині цього ряду, і буде серединним відхиленням.
Якщо ряд всіх відхилень складається з парного числа відхилень, то для визначення величини серединного відхилення потрібно взяти два відхилення, які стоять посередині, і розділити суму їх абсолютних величин на два.
Приклад. Шести пробоїн відповідають такі величини відхилень від осі розсіювання по висоті: вище осі розсіювання 4-15; +25; +70 см; нижче її - 10; - 40; - 60 см. Визначити серединне відхилення по висоті (Вв),
Рішення. Виписавши по абсолютній величині все відхилення в порядку зростання, отримаємо: 10; 15; 25; 40; 60; 70 см.
Дійсно, відхилення 32,5 см більше кожного з перших трьох відхилень і менше кожного з останніх трьох відхилень.
Примітка. При невеликому числі вимірювань визначення величини серединного відхилення таким способом не забезпечує необхідної точності, так як отримання одного додаткового відхилення може значно змінити величину серединного відхилення для одного і того ж способу стрільби.
Приклад. Якщо до ряду відхилень, зазначених у попередньому прикладі, додати ще одне відхилення, рівне 80 см, то серединне відхилення стане рівним 40 см (10; 15; 25; 40; 60; 70; 80).
У цих випадках величина серединного відхилення більш точно обчислюється за допомогою середнього арифметичного значення. Серединне відхилення дорівнює 0,84 або округлено 5/6, середнього арифметичного значення.
Середнє арифметичне значення визначається діленням суми абсолютних значень усіх відхилень на кількість відхилень. Так наприклад, за умовами попереднього прикладу середнє арифметичне значення дорівнює
а серединна відхилення
У цих випадках враховуються чисельні значення всіх відхилень, і результати окремих відхилень не позначаються так значно на величині серединного відхилення.
Серединне відхилення може бути обчислено також за допомогою середнього квадретіческого значення. Серединне відхилення дорівнює 0,67 або округлено 2/3 середнього квадратичного значення.
Середнє квадратичне значення при невеликому числі відхилень дорівнює кореню квадратному із суми квадратів відхилень, поділеній иа число всіх відхилень без одного.
Так, за умовами попереднього прикладу середньоквадратичне значення дорівнюватиме
а серединна відхилення
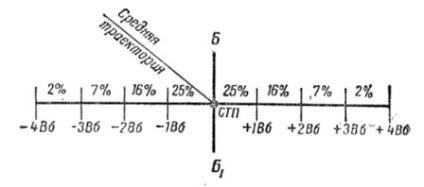
Мал. 26. Шкала розсіювання по бічному напрямку
з масштабом в одне середнє відхилення
69. Якщо від тієї чи іншої осі розсіювання відкласти в обидві сторони послідовно смуги, рівні по ширині відповідному серединному відхиленню, то вся площа розсіювання виявиться розділеною на вісім рівних смуг - по чотири в кожну сторону, а повне розсіювання з будь-якого напрямку буде дорівнює восьми серединним відхилень.
Насправді можуть бути відхилення від центру розсіювання, що перевищують чотири серединних відхилення, але ймовірність отримання їх мала (не перевищує 0,7%).
При великому числі пострілів в кожній з смуг, що дорівнює по ширині одному серединному відхилення або його частини, незалежно від величини розсіювання міститься певний відсоток точок зустрічі (попадань).
Креслення, що показує процентний розподіл попадань в смуги, рівні по ширині одному серединному відхилення або його частини, називається шкалою розсіювання (рис. 26). Шкала розсіювання в чисельному вираженні однакова з будь-якого напрямку і характеризує закон розсіювання.
Для смуг шириною в одне серединне відхилення міститься (округлено): в перших шпальтах, що примикають до осі розсіювання, по 25% точок зустрічі, по-друге по 16%, в третіх за 7% і в крайніх по 2%.
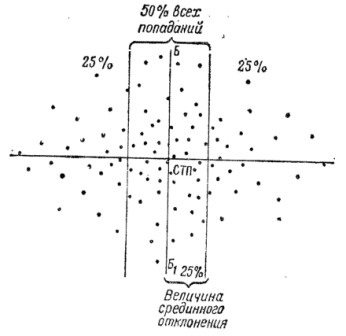
Мал. 27. Визначення величини середнього відхилення
по боковому напрямку графічним способом
Для смуг, ширина яких дорівнює сотій частині серединного відхилення, відсотковий розподіл попадань зазначено в табл. 1 додатка 4.
70. При великому числі влучень (точок зустрічі) величину серединного відхилення можна визначити графічним способом (рис. 27). Для цього відраховують справа (зверху) 25% влучень (точок зустрічі) і відокремлюють їх вертикальної (горизонтальної) лінією; відраховують зліва (знизу) 25% влучень (точок зустрічі) і також відокремлюють їх вертикальної (горизонтальної) лінією. В результаті цього вийде смуга, що вміщає 50% влучень (точок зустрічі), т. Е, смуга кращої половини попадань. Потім вимірюють відстань між вертикальними (горизонтальними) лініями. Половину відстані між вертикальними (горизонтальними) лініями приймають за величину серединного відхилення. У зв'язку з цим іноді користуються іншим визначенням серединного відхилення: серединним відхиленням називається половина
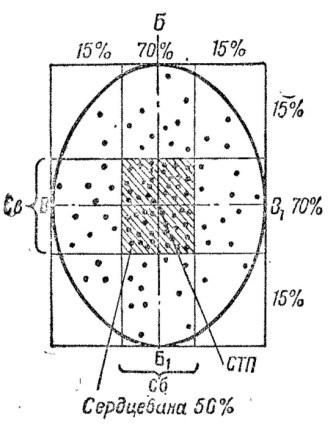
Мал. 28. серцевина смуги і серцевина розсіювання
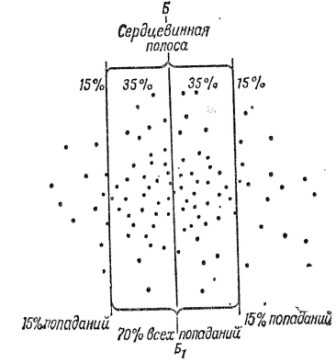
Мал. 29. Визначення величини серцевина смуги по боковому напрямку графічним способом
ширини центральної смуги розсіювання, що вміщає 50% всіх влучень, за умови, що вісь розсіювання проходить по її середині.
71, Смуга розсіювання, що містить в собі 70% влучень (точок зустрічі), за умови, що вісь розсіювання проходить по її середині, називається серцевиною смугою (рис. 28).
Серцевинні смуги позначаються: Сд - серцевинна смуга по дальності; Св - серцевинна смуга по висоті; Сб - серцевинна смуга по бічному напрямку.
При перетині двох серцевинних смуг утворюється прямокутник, що включає в себе кращу, найбільш купчасто половину всіх точок зустрічі (0,70-0,70 = 0,49, округлено 0,50, або 50%).
Прямокутник, утворений перетином двох серцевинних смуг, називається серцевиною розсіювання.
Ширина серцевинною смуги може бути визначена графічним способом (рис. 29). Для цього треба відрахувати
справа (зверху) 15% влучень (точок зустрічі) і провести вертикальну (горизонтальну) лінію; відрахувати зліва (знизу) 15% влучень (точок зустрічі) і також провести вертикальну (горизонтальну) лінію. В результаті цього вся площа розсіювання виявиться розділеною на три майже рівні смуги, при цьому центральна смуга містить 70% влучень, а крайні - по 15% кожна. Потім слід виміряти відстань між вертикальними (горизонтальними) лініями, яке і буде одно шіріне.сердцевінной смуги.
Між серцевинною смугою і серединним відхиленням як заходами розсіювання є певна залежність. Серцевинна смуга включає в себе 3,06 відповідного серединного відхилення. На практиці ширину серцевинною смуги приймають округлено дорівнює трьом середнім відхиленням.
72. При стрільбі па близькі відстані площа розсіювання на вертикальній площині має форму кола, що означає приблизна рівність характеристик розсіювання по висоті і по бічному напрямку. Тому про величину такого розсіювання іноді судять не за двома параметрами (Вв і Вб або Св і Сб), а по одній величині - радіусу кола, що вміщає кращу половину (Р50) всіх попадань або все (Р100) попадання.
Для визначення величини радіусу кола, що включає 50 або 100% влучень, необхідно (рис. 30) визначити середню точку влучення. Потім, приймаючи середню точку влучення за центр кола, провести циркулем коло так, щоб вона вмістила половину (50%) або все (100%) точки зустрічі. Розчин циркуля дає в першому випадку величину радіуса кола, що включає 50% а в другому - 100% влучень.
Радіус кола, що вміщає все попадання, приблизно в 2 1/2 рази більший за радіус кола, що вміщає кращу половину влучень.
Між величиною радіуса кола, що вміщає кращу половину влучень, серединними відхиленнями і серцевинними смугами є певна залежність. Радіус кола, що вміщає кращу половину влучень (50%), дорівнює 1,76 серединного відхилення або 0,6 серцевинною смуги.
73. Між величинами розсіювання по дальності і по висоті є певна залежність: розсіювання по
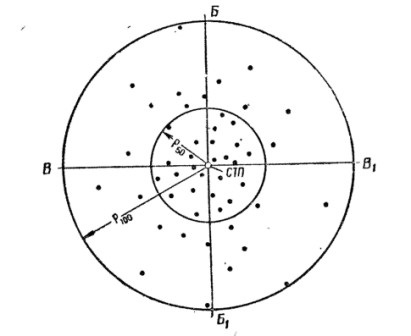
Мал. 30. Визначення величини радіусів кіл, що вміщають 50 і 100% влучень
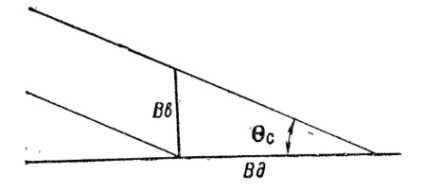
Мал. 31. Залежність між середніми відхиленнями по дальності (Вб) і по висоті (Вв)
дальності одно розсіюванню по висоті, помноженому нз 1000 і розділеному на величину кута падіння в тисячних (рис. 31), т. е,
Прімер.Определіть bд, якщо Вв = 0,36 м, а кут падіння 10 тисячних.